1. 引言
实验上,利用现代材料生长技术,比如,分子束外延生长(molecular beam epitaxy,简记为MBE)、金属有机化学气相沉积(metal-organic chemical-vapor deposition,简记为MOCVD)等,可以构筑重要的磁纳米结构 [1],例如,在半导体GaAs/AlxGa1-xAs异质结表面上沉积铁磁(ferromagnetic,简记为FM)条带等 [2]。在磁纳米结构中,磁性材料产生不均匀的磁场,局域地影响半导体内高迁移率二维电子气(two-dimensional electron gas,简记为2DEG)的运动。由于小尺度、低维度和量子磁受限,磁纳米结构中蕴藏着新奇的量子效应 [3],例如,自旋极化 [4] [5] [6]、巨磁阻(GMR) [7] [8] [9] 和古斯–汉兴(Goos-Hänchen)效应 [10] [11] [12] 等。这些新颖的量子效应可以被广泛地用于设计和开发新型的纳米及量子电子器件,比如,自旋过滤器 [13] [14] [15]、空间自旋分离器 [16] [17] [18]、GMR器件 [19] [20] [21] 等。因此,磁纳米结构中量子效应及其器件的设计已经成为凝聚态物理、材料物理、半导体器件等领域中的研究热点。
近年来,磁纳米结构中的波矢过滤(wave vector filtering,简记为WVF)效应 [22] 吸引了研究人员的广泛关注,因为其本身的科学意义以及在开发纳米电子动量过滤器(momentum filter)中具有潜在的应用价值。在2017年,选取一个真实的磁纳米结构——可通过在半导体GaAs/AlxGa1-xAs异质结表面上沉积具有垂直磁化强度的纳米FM条带在实验上制备,Lu等人 [23] 率先研究了波矢相关的输运以及δ-掺杂的影响,发现电子具有相当大的WVF效应,而且其程度(即WVF效率)可通过改变δ-掺杂的权重或位置进行有效的调控,因此,基于该磁纳米结构,他们成功地提出了一个纳米电子动量过滤半导体器件。随后,另一个真实磁纳米结构 [24] 及其简化结构 [25] 中电子的WVF效应的δ-掺杂的调控也被研究,支持了文献 [23] 的研究结果,并设计了一个新的结构可控的电子动量过滤器。考虑一个磁、电受限半导体异质结构 [26] ——实验上通过在半导体GaAs/AlxGa1-xAs异质结上、下表面分别构筑FM条带与肖特基金属(Schottky metal,简记为SM)条带实现,其电子的WVF效应被报道,并发现它的效率可通过改变SM条带参数进行控制 [27]。利用原子层掺杂技术,Liu等人 [28] 进一步研究了δ-掺杂的影响,建议了一个结构可控的电子动量过滤器。Kong等人 [29] 施加偏压到系统上、激发一个横向电场,发现通过改变电场的方向或强度可以有效地操控该磁、电受限半导体异质结构中电子的WVF效应,结果提出了一个电可控的纳米电子动量过滤半导体器件。近期Zhang等人 [30] 研究了一个新奇的磁纳米结构,其具有零平均磁场、并可通过在半导体异质结上、下表面沉积3个具有垂直磁化强度的FM条带实现,为纳米电子学器件的应用提出了一个新的电子动量过滤器。
受到上述研究工作的激励,本文研究另一个磁、电受限半导体异质结构 [31] 中电子的WVF效应。实验上,这个磁纳米结构可以通过在半导体GaAs/AlxGa1-xAs异质结的表面上,平行地沉积FM条带与SM条带制备。我们发现系统中存在一个相当强的电子WVF效应,而且其WVF效率与SM条带的位置、宽度及应用门控电压有密切的关系。因此,基于这个磁纳米结构,我们设计了一个新的纳米电子动量过滤半导体器件。
2. 结构模型和理论方法
本文考虑的磁、电受限半导体异质结构 [32] 被大体上画在图1(a)中,这里具有水平磁化强度(
)的FM条带和施加负直流电压(
)的SM条带被平行地沉积在半导体GaAs/AlxGa1-xAs异质结的表面上 [33] [34];图1(b)表示它的结构模型。

Figure 1. (a) Magnetically and electrically confined semiconductor heterostructure and (b) Its structural model
图1. (a) 磁、电受限半导体异质结构构筑图和(b) 它的结构模型图
在图1中,参数
和
分别代表FM条带和SM条带的宽度,D是两条带之间的距离,
表示SM条带的中心位置坐标。如果FM条带与2DEG平面之间的距离很小,水平磁化的FM条带产生的、作用于2DEG的磁场轮廓通常可以用两个反方向的δ-函数形状的磁垒来近似 [5],即:
, (1)
式中B是δ-磁垒的磁感应强度,δ(x)是Delta函数。采用Landauer规范,对应的磁矢势可以表示为
,其中 [35]:
, (2)
式中
是磁长度,
表示一个典型的磁场。当2DEG材料的电阻率各向同性并且SM条带到2DEG平面的距离很小时,施加了负压的SM条带在2DEG平面上产生的电势,导致一个近似的方形电势垒,如:
, (3)
其中
表示方形电势垒的高度,
是Heaviside阶跃函数。
在单电子、有效质量近似,磁、电受限半导体异质结构中电子的Hamiltonian算符可表示为:
, (4)
式中,
、
、
和
分别表示电子的有效质量、自由质量、动量和有效朗德因子,
是Pauli算符的z分量、对应于自旋向上/自旋向下电子。需要指出的是,在方程(4)的右手边的最后一项表示电子自旋与结构中磁场的相互作用,即Zeeman耦合项,对于GaAs材料(
和
)该项的值很小,其对电子在磁、电受限半导体异质结构中的输运性质影响可以忽略 [36]。由于电子在磁纳米结构中沿y方向的运动没有限制,其定态Schrödinger方程
的解,可以写为
,其中
是电子波矢的y分量(即纵向波矢),波函数
满足下面的一维(1D) Schrödinger方程:
, (5)
其中,电子在磁、电受限半导体异质结构中所感受到的有效势为 [37]:
(6)
该有效势不仅与纵向波矢有关,而且与SM条带有关。有效势对ky的依赖性,使电子在磁纳米结构中的隧穿本质上是一个二维(2D)过程,导致了磁纳米结构中的WVF效应 [22];而有效势依赖于SM条带,使通过改变SM条带的宽度、位置和应用电压调控磁、电受限半导体异质结构的WVF效应成为可能 [27]。
利用改进的转移矩阵法(improved transfer matrix method,简记为ITMM) [6],可以严格求解1D Schrödinger方程(5)。为此,把整个磁、电受限半导体异质结构分成入射区I、结构区(II、III、IV)和透射区V,如图1(b)所示。在I与V区,电子的波函数可分别假设为
和
,其中
,
是反射波/透射波的幅度。在结构区,电子的波函数是平面波的线性组合,即:
(7)
其中三个区的波矢分别为
,
和
,而
和
是六个待定常数。利用波函数及其一阶导数在各区边界[
和
]连续的条件,借助于ITMM方法 [6],可以得到:
(8)
其中,
,
,以及
(9)
因此,电子通过该磁、电受限半导体异质结构的透射系数为
(10)
透射系数对纵向波矢微分,可以计算表征WVF效应程度的WVF效率,即 [23]:
(11)
3. 结果与讨论
作为电子入射能量的函数,图2(a)展示了电子通过图1所示磁、电受限半导体异质结构的透射系数,图中结构参数取为
、
、
、
、
和
,电子的纵向波矢为
(实线)、0.0(虚线)和
(点线)。由于电子在磁纳米结构中的传输本质上是二维过程,电子透射系数关于纵向波矢的各向异性可以从这个图清楚地观察到。当电子纵向波矢从负值向正值变化时,它的透射系数值减小,透射谱略微向高能方向移动。在低能区,透射谱上出现一个共振峰,那是因为此时电子的有效势等效于对称的双垒结构,电子的入射能量大约等于势阱内的束缚能级、发生了共振隧穿。电子通过磁、电受限半导体异质结构的透射系数随纵向波矢的变化特点,可以从其有效势对纵向波矢的依赖性得到理解。为了更清楚地观察电子透射的各向异性,在该图的插图中我们给出了电子透射系数随其纵向波矢的直接变化,图中电子的入射能量取为2.04 meV。的确,从这个插图我们可以清楚地看到,电子的透射系数随着它的纵向波矢剧烈地变化。这个现象表明,我们考虑的磁、电受限半导体异质结构具有很强的电子WVF效应。在图2(b)中,我们计算了电子WVF效率,图中电子的纵向波矢仍然取为
(实线)、0.0(虚线)和
(点线)。相当大的WVF效率可以被看到,比如,当电子的纵向波矢
时,在入射能量
处,WVF效率可达到−1.65左右。
考虑到在磁、电受限半导体异质结构中,电子的有效势与结构中SM条带的参数密切相关[参见式(6)],接下来研究通过改变SM条带的应用电压产生的电垒(
)、位置(
)、宽度(
)等对电子的WVF效应调控。为了突出SM条带的影响,下面的讨论中电子的纵向波矢被固定为
,即仅考虑电子正入射的情况。首先,把SM条带的宽度和位置固定为
和
(此时FM条带与SM条带相距
),来研究施加在SM条带上的负直流电压(
)在2DEG内产生的电垒高度(
)对WVF效应的影响。在图3(a)中,我们展示了电垒高度分别为
(实线)、1.02 meV (虚线)和1.70 meV时电子的WVF效率。这个图清楚地显示,电子在磁电受限半导体异质结构中的WVF效率与结构中SM条带上的应用电压密切相关。一般地,当电垒变高,电子的WVF效率会增加,而且η-E曲线向高能方向移动。所以,我们可以通过改变施加在SM条带上的直流负压的大小,控制磁、电受限半导体异质结构中电子WVF效应的程度,这是因为电子的有效势依赖于SM条带上应用的电压。而且,电子WVF效应对电垒高度的依赖性,与电子的入射能量有关,特别是在1.02 meV至3.06 meV的能量范围内更为明显。为了更清楚地观察电垒高度的影响,直接作为
的函数我们计算了电子的WVF效率,如图3(b)所示,图中电子的能量
(实线)、2.04 meV (虚线)和3.06 meV (点线)被考虑。这个图的三条曲线,特别是低能量1.02 meV的结果,都明显的反映出电子的WVF效率随着SM条带上应用电压产生的电垒剧烈地变化。这个特点将导致我们考虑的磁、电受限半导体异质结构,可以被设计成电可控的电子动量过滤器,其过滤效率可通过SM条带上施加的电压进行调节。

Figure 2. (a) Transmission Coefficient and (b) WVF efficiency
图2. (a) 透射系数和(b) WVF效率

Figure 3. WVF efficiency varies with (a) Incident energy and (b) SM electric-barrier height, respectively
图3. WVF效率随(a) 入射能量和(b) SM电垒高度变化
然后,保持应用电压(
)或电垒高度(
)不变,比如
,改变SM条带的位置(
)及宽度(
),探索SM条带对系统中电子WVF效应的操控。在图4中,SM条带的宽度被固定为
,我们展示了SM条带的位置对电子WVF效应的影响,其中图4(a)给出了3个具体的宽度
(实线)、28.75 nm (虚线)和34.5 nm (点线)情况下电子的WVF过滤效率。从这些曲线,我们看到WVF效率随着电子的入射能量振荡式的变化,特别是,当能量在1.02 meV至5.1 meV范围内更为剧烈。更重要的是,当SM条带的位置变化时,系统中电子的WVF效率发生明显的改变。我们看到,当
增加,即SM条带远离磁、电受限半导体异质结构的中心时,WVF效率显著的提高,而且η-E曲线向低能方向移动。SM条带的位置对WVF效应的影响,可以从图4(b)上看得更加清楚,因为该图直接展示了WVF效率随着SM条带的位置的变化,其中电子的入射能量被取为
(实线)、3.06 meV (虚线)和4.08 meV (点线)。的确,SM条带对系统中电子的WVF效应有重大的影响,而且其与电子的入射能量有很大的关系,尤其是在能量
的时候。换言之,我们可以通过恰当地沉积SM条带在磁、电受限半导体异质结构中的位置,使得系统中电子的WVF效应最强,从而设计最佳的电子动量过滤器。显然,SM条带位置对WVF效应的控制作用,源于电子在系统中感受到的有效势(
)对SM条带位置(
)的关联性。
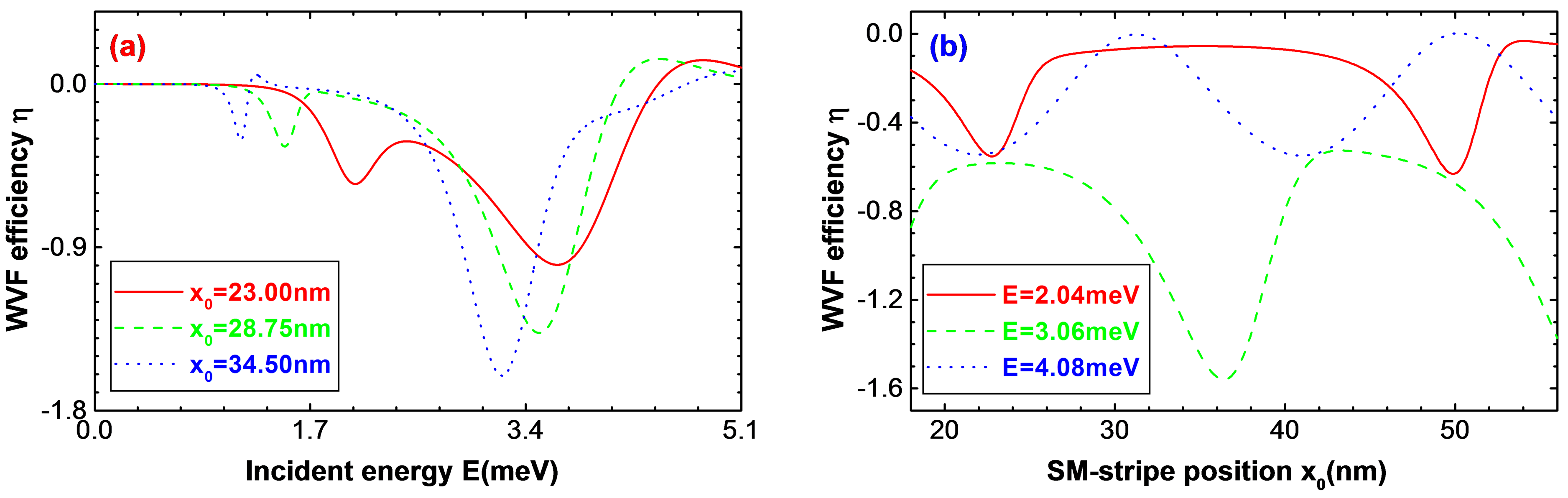
Figure 4. WVF efficiency varies with (a) Incident energy and (b) SM-stripe position, respectively
图4. WVF效率随(a) 入射能量和(b) SM-条带位置变化
事实上,电子的有效势除了依赖于位置,其还与SM条带的宽度有关,因此宽度对电子的WVF效应也将有重大的影响。最后,在图5我们给出了图1所示的磁、电受限半导体异质结构中电子WVF效率与电子的入射能量的关系,图中我们考虑了3个具体的SM条带宽度
(实线)、34.5 nm (虚线)和46.0 nm。

Figure 5. WVF efficiency changes with incident energy and SM-stripe width (in the inset), respectively
图5. WVF效率随入射能量及SM-条带宽度(插图)的变化曲线
从这个图,我们可以观察到,SM条带的宽度对系统中电子的WVF效应有一个重大的影响。当SM条带的宽度变宽时,电子的WVF效率被大大地改变了,而且其随电子能量变化的曲线向低能端发生移动。SM条带的宽度对系统中电子的WVF效应的影响,被更加清楚地反映在图5的插图中,这里电子的WVF效率(
)直接作为SM条带宽度(
)的函数被计算,其中电子的入射能量被选择为
(近似为电子的费米能级)。确实,由于电子在磁、电受限半导体异质结构(参见图1)中经历的有效势[方程(6)]与SM条带的宽度密切相关,因此WVF效率随SM条带的宽度剧烈地变化。SM条带宽度对电子WVF效应的影响表明了,我们也可以通过改变SM条带的宽度,实现对系统中电子WVF效应的调控,即设计可控的电子动量过滤器。
4. 结论
总之,本文从理论上研究了一个磁、电受限半导体异质结构中电子的WVF效应,提出了可控的电子动量过滤器。该磁、电受限半导体异质结构,可通过在GaAs/AlxGa1-xAs异质结的表面上,平行地沉积纳米FM和SM条带在实验上构筑。由于电子在磁纳米结构中的运动本质上是一个二维过程(与纵向波矢有关),因此该磁、电受限半导体异质结构中出现了一个明显的WVF效应。而且,由于电子在系统中所感受到的有效势与SM条带密切相关,所以通过改变SM条带的位置、宽度及施加的负压(电垒高度),可以调控系统中电子的WVF效率的大小,从而为纳米电子学器件的应用开发可调的电子动量过滤器。
基金项目
湖南省教育厅科学研究基金(批准号:18C1290)资助的课题。
NOTES
*通讯作者。