1. 引言
滑动轴承是一种应用于大型转子机械及特殊工况机械的一种重要部件，其中滑动轴承的轴心轨迹能够直接反映轴承的工作状态，通过轴承的轴心轨迹可以判定轴承的稳定性 [1] 。了解轴承的润滑状况，验证轴承设计参数的合理性 [2] ，是衡量滑动轴承性能的重要性能指标之一。因此滑动轴承的轴心轨迹的研究具有十分重大的工程意义。
在轴心轨迹研究方面，Hahn [3] 首先提出静力学方法，但由于模型过于简化，所得结果与实际情况相差甚远。裘祖干 [4] 提出一种动载滑动轴承轴心轨迹的动力学计算方法，,即将轴承–润滑油膜–轴颈作为一个运动系统，在求解轴心轨迹时引入运动件的动量方程，这一结果更接近轴承实际运行状况。在求解轴承油膜力的过程中Hahn和裘祖干采用的均是是有限差分法，一般情况下有限差分法具有较高的精度，但是在处理复杂的几何形状和考虑油膜形状和物性的不连续上显的不足 [5] 。吴刚在研究滑动轴承轴心轨迹的可视化研究方案时，采用了无限长轴承理论 [6] ，这种假设能够给求解油膜力带来很大方便，但是在求解精度上会大打折扣。刘大全提出了求解油膜力的一维解法 [7] ，但是其将油膜破裂边假设为直线的方法忽略了油膜破裂边的非线性，与实际油膜力并不符。
求解瓦块油膜力是计算轴颈轴心轨迹十分重要的一环，本文针对前人研究方法的缺陷，在求解油膜力之精度与适应性的基础上，利用动载滑动轴承的动力学计算方法，求得五瓦可倾瓦滑动轴承的轴心轨迹。因有限单元法对特殊形状具有较好的适应性，九节点四边形单元可以以较少的单元获得较高的精度，所以本文采用九节点四边形单元的有限元方法求解Reynolds方程，得到油膜压力并积分得到油膜力，然后求解运动方程，得到轴颈瞬时加速度，再采用欧拉方法计算轴承下个时刻速度和位置，直到求得完整的轴心轨迹。仿真结果表明：用有限元法求解轴心轨迹能实现预期结果，并具有较好的普适性，在一般结构轴承和特殊结构轴承上均具有推广价值。
2. 有限元方法
2.1. Reynolds方程
不可压缩、层流状态下动载荷作用无量纲雷诺方程为：
(1)
为润滑油粘度；h为油膜厚度；
为轴颈转速；
为从x周正向量起的油膜角；
为轴向坐标；
为径宽比。
油膜厚度为
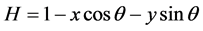
其中：除ω外，其它量均为无量纲量H，x，y的量纲比为轴承半径间隙C，
，
的量纲比为
。
2.2. Reynolds方程的有限单元法 [8]
将黏度视为常数，Reynolds方程等价泛函L(p)为：
(2)
由变分原理知，Reynolds方程的解p应该满足
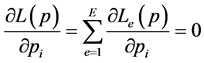
即
(3)
式中
为第i个节点压力，e为任意四边形单元，E为单元总数。
将所有单元都转换成局部坐标系下的正方形标准单元。则可用插值函数表达各量为：
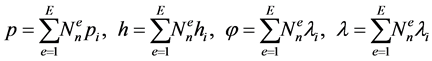
式中，
，
，L为整个解区域的节点总数；
为第e个单元内第n个节点的插值函数；ξ、η为局部坐标，hi、φi、λi分别为第i个节点的相应值。上标e表示对应单元内节点的值。
记：
，
，
逐单元积分后，对流量矩阵进行组装，得到对应的总刚矩阵K和载荷矩阵B，则压力P：
(4)
图1为利用有限元方法，求解的静态二维油膜力。其参数如表1所示，所采用的是40 × 10的九节点四边形单元。
2.3. 可倾瓦滑动轴承瓦块姿态计算
五瓦可倾瓦轴承示意图如图2所示，可倾瓦轴承每块瓦块可以绕瓦块支点转动，各瓦相互独立，各瓦能够根据受力情况调整姿态，这也是可倾瓦轴承的优势所在。图3为轴承坐标系及其瓦块展开图，
表示油膜正压力区及油膜破裂区，
为油膜域
的边界，及
的交界线，轴颈中心为
，轴承中心为
，润滑域在动载情况下具有不确定性。
在计算单瓦油膜力时需要考虑瓦块的摆动，要求解瓦块压力，需要先确定瓦块的姿态和轴心坐标的相对位置。也就是求偏位角
值。此处为了简化计算，利用相对运动，把寻找β值转换为改变轴心的相对位置，试探性的微小改变轴心的x坐标，并在当前x坐标小计算得到压强值对枢轴的力矩
(5)
如果计算得到的力矩M不为零，则继续改变轴颈中心的x坐标，并计算相应的压强值，利用方程(5)计算力矩，直到M为零，其中
为瓦块第j个单元所对应的角度。同时还要考虑轴颈位置的改变是有极限位置的，无量纲化后，即是
。此时，按照当前x坐标下计算得到的压强值就是第i块瓦块的压强分布。求得相对位置后油膜力的计算方法与固定瓦相。
表1. 轴承参数
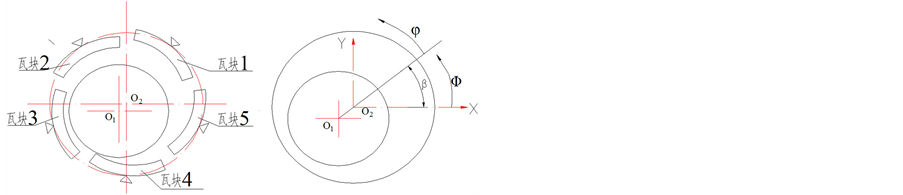
Figure 2. The structure of tilting pad
图2. 可倾瓦轴承结构示意图
Figure 3. The coordinate of the bear
图3. 轴承坐标系及其瓦块展开图
3. 轴承系统模型
3.1. 运动方程
根据方程(4)可计算得到油膜压力
，再通过积分得到油膜在x, y轴方向的合力
，假设轴颈在运动过程中不与轴瓦接触，则轴颈在运动过程中所受到的力有轴瓦的支反力和不平衡质量引起的离心力。根据牛顿运动定律，轴颈的运动方程无量纲形式可以写为如下形式：
(6-1)
(6-2)
上式中，各量都是无量纲量，a的量纲比为
；b的量纲比为
；C为轴承的无量纲阻尼；K为轴承的无量纲刚度；
，
为第i块瓦在X和Y方向的分量，量纲比为
；右边最后一项为存在质量偏心时的不平衡离心力在X和Y方向的分量；
，
量纲比为
。
3.2. 轴心轨迹
由于考虑了轴的惯性力和油膜力
，
的非线性，所以这种轨迹计算方法属于轴心轨迹的非线性分析，其计算步骤如下：
1) 设定初始的轴颈状态，
，计算压力p，油膜力
，
。但应考虑到轴心位置X，Y，存在
。
2) 将计算得到的
，
，代入公式(6-1)，(6-2)，计算得到加速度
，
。
3) 用欧拉法计算轴下一时刻的状态，即
时间后，轴心的速度和位置
和
。
(7)
4) 计算得到
和
在回到1)，反复计算1)~3)，直到循环收敛或者小范围波动。
4. 动载荷作用下的油膜力和轴心轨迹
以图2所示的五瓦可倾瓦滑动轴承为例，设定其参数如表2所示。
4.1. 阶跃载荷作用下的轴心轨迹
为了研究了阶跃载荷作用下的轴心轨迹运动规律，本文取不平衡力的变化规律如公式(8)所示，
(8)
图4是在阶跃载荷的作用下，轴颈中心的运动轨迹，在开始阶段qx为0，轴心在自重和油膜力的作用下达到一个平衡点，即图示的1号平衡点。在16π的时间开始不平衡力x方向上的分力突然增加，而y方向上的分力不变为0，此时轴心必须找到一个新的平衡点，即2号平衡点，经过一段时间后轴颈开始平衡于2号平衡点。图5是轴颈中心分别在X和Y方向上轴颈中心的位移，从图5能够直观的看出，两个方向上的位移都出现了两个波动过程，波动出现的原因子图4中已经分析，从该图中能够更加清晰的知道稳定后的轴颈处于一个十分平稳的状态。
为了验证结果正确性，参考文献 [5] 所得的固定瓦滑动轴承在阶跃载荷作用下的轴颈中心运动规律，为了保持验证的可靠性，除固定瓦和可倾瓦的区别外，其他参数如载荷，径宽比，轴质量，转速等设置均一致，图6和图7为文献 [5] 得到的轴心轨迹图和轴心位移图，从两幅图看出在阶跃载荷作用下固定瓦
Table 2. The parameter of tilting pad
表2. 可倾瓦轴承参数
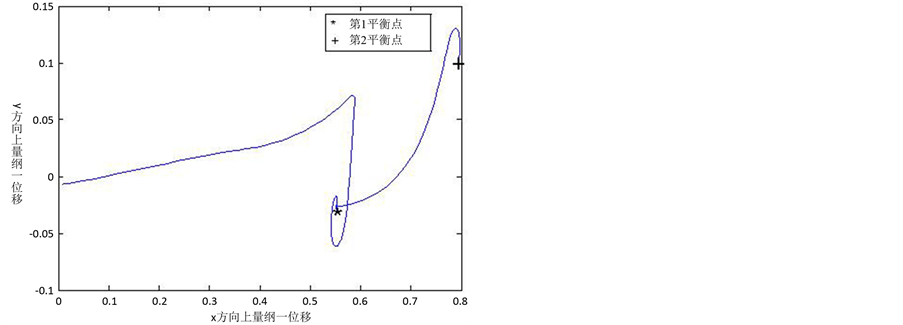
Figure 4. The shaft orbit under step load
图4. 阶跃载荷作用时的轴心轨迹
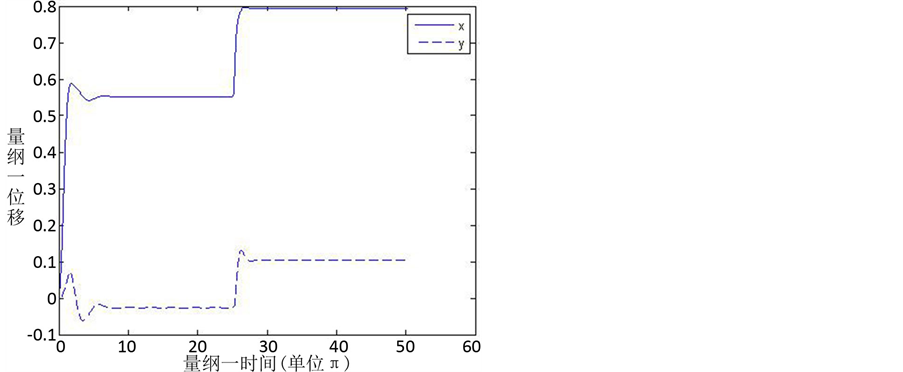
Figure 5. The displacement on X and Y
图5. X和Y方向的位移
轴承收敛于两个平衡点且当载荷发生变化的时候会出现短暂的波动，和有限差分法所得的轴颈中心运动规律完全一致。
4.2. 交变载荷作用下的轴心轨迹
改变不平衡力取
；
，图8为轴颈的轴心轨迹图，该图可以直观的看出轴心的运动轨迹，从图中可知，轴心初始阶段偏离平衡位置较远，但是经过一段时间后，逐渐趋于稳定，且稳定后的成8字型。图9分别为轴颈轴心在x轴和y轴方向的位移波形图，从中可以分别看出轴心位移在x和y方向分量的变化关系。结合三图可见，轴在一开始会经历一段时间的振荡，此时处于不稳定运转时期，轴心轨迹偏差较大，大概在经历650个时间步长后稳定下来，此时轴处于稳定运转时期，轴心轨迹趋于一致。图10为各瓦块1在油膜力对称轴处的压力，也即最大压力处随时间的变化关系图(图中
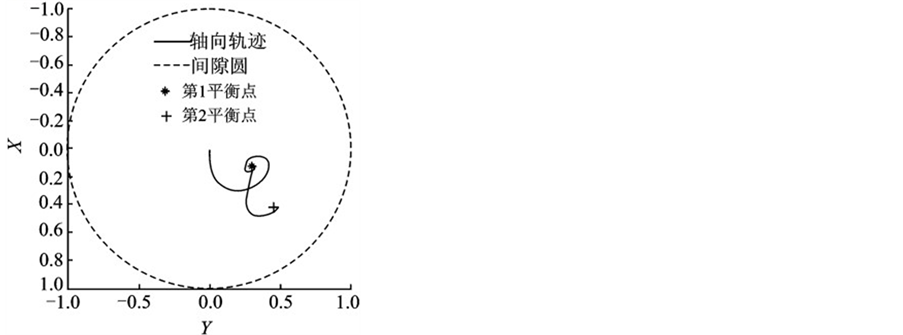
Figure 6. The shaft orbit under step load
图6. 阶跃载荷作用时的轴心轨迹
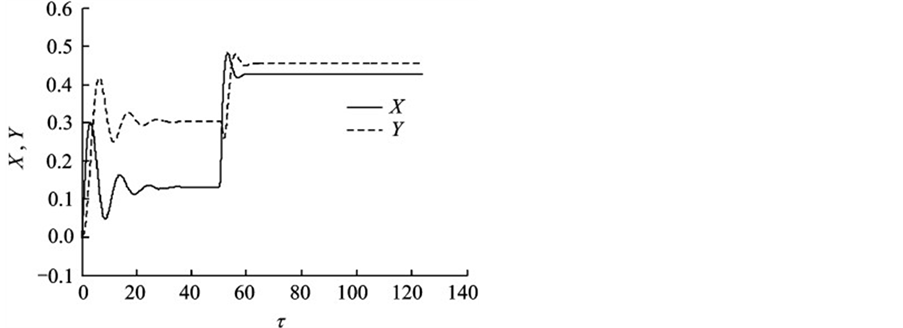
Figure 7. The displacement on X and Y
图7. X和Y方向的位移
取稳定后的100个时间步长)，该图可以直观的看出各瓦块油膜力相互调整的关系及各瓦块油膜力随时间的变化关系，结果显示各瓦块最大油膜力分布在时间轴均呈比较规则的周期变化的关系，这与轴心位移
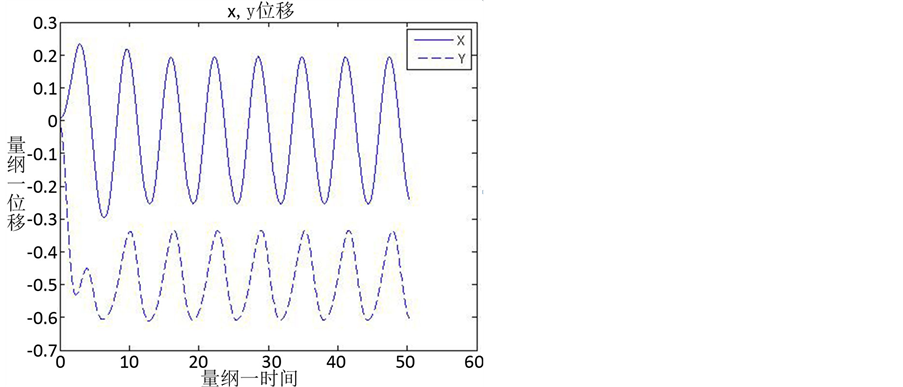
Figure 9. The displacement in x and y direction
图9. x，y方向位移
在稳定后呈周期变化关系相符。
5. 小结
1) 运用有限元方法计算滑动轴承油膜力的数学模型，通过设定一组瓦块参数，用四边形九节点单元的有限元方法运算，得到了瓦块的二维油膜压力分布。
2) 建立了一种求可倾瓦滑动轴承瓦块轴颈相对衡位置的有限元计算方法。根据相对运动的理念，将瓦块的摆动转化为轴颈中心的运动，通过x轴的微小位移来达到平衡。但由于此过程是将瓦块的近似为直线求矩，故假设会带来一定程度的误差，但不影响对轴颈振动规律的研究。
3) 模拟了一种工况下轴心轨迹的运动，轴心轨迹在启动阶段会存在一段时间的涡动期，在经过一段时间的调整后会进入平稳运转时期，此时x轴，y轴位移波动较小，呈一条有规律的正弦曲线。轴承最终达到平衡是各瓦油膜力相互相调整的一个过程，稳定后，油膜力随时间呈周期性变化。
4) 用有限元方法能够得到理想的轴心轨迹。这种方法能够利用有限元方法适应性好的优势，处理各种复杂的油膜。