1. 引言
极光是磁层-电离层相互作用的最集中的表现形式,是唯一能够用肉眼看得见的具有极区特征的地球物理现 [1] 。通过系统地观测极光形态可以获得大量关于磁层和日地空间电磁活动的信息,有利于研究太阳活动对地球影响进而了解空间天气变化规律。同时极光也是一种无线电现象,它的产生直接影响到人类的无线电通讯 [2] 。除此之外,极光对气候也会有一定影响,因此会影响到生物学过程。由此看出,极光研究以及极光的观测已成为世界各国极地高空大气物理研究的重要课题。
早期的极光分类是基于肉眼观察进行的手工标记和分类 [3] ,直到2004年,随着计算机技术的发展,计算机视觉技术、模式识别等技术应用到极光分类研究领域中,实现了极光图像的自动分类和检测。对于极光的分类研究,早期主要包括:1955年,Carl Stormer [4] 开创了极光分类的先河,将极光分为放射状结构、无放射状机构以及火焰状结构,还对这三个大类进行了详细的划分。1964年,Akasofu [5] 将极光基于过程分为赤道向扩展、点亮、西行浪涌、赤道向恢复等不同类型。1999年,Hu [6] 将极光分为具有射线状结构的冕状极光、带状极光、极光涌浪以及向日极光弧等四个类别来进行分析。利用有监督分类方法,Syrjäsuo和Donovan [7] [8] [9] 等人以及 Wang [10] 等人都实现了对极光图像的自动分类。2004 年,Syrjäsuo [7] [11] 等根据图像模式识别等技术将夜侧极光进行了自动分类及检索。将夜侧极光分为弧型(Auroral arcs),斑块型(Patchy auroras)和欧米伽(Omega-bands)。这些研究都是在极光图像检测的基础之上,2002年Syrjäsuo和Donovan [12] 用kNN分类器实现了有无极光的分类,达到了专家判别结果的90%,并提出一种成功追踪极光弧的算法,2012年,Syrjäsuo [13] 分别从简单强度特征 [14] 、纹理特征 [10] [14] [15] [16] 和亮度不变特征 [17] 角度对极光图像特征提取,实现了极光图像的自动检测,其中,基于纹理特征的LBP的方法取得了不错的检测效果。然而这种方法的抗噪性较差,在图像旋转或者平滑滤波的情况下结果也会明显下降。
为了提高极光图像在加噪、旋转、平滑滤波后的检测效果,文章提出了一种基于图像的Zernike矩的极光检测的方法。由于连续正交的Zernike矩是定义在极坐标下的,因此本身具有旋转不变性。通过实验表明,在图像添加噪声、旋转以及平滑滤波后,基于Zernike矩的特征提取方法比LBP [18] 的检测效果好。
1.1. Zernike矩特征
1.1.1. Zernike矩 [19]
对于极坐标表示的图像函数 ,其n阶
,其n阶 重的Zernike矩定义为:
重的Zernike矩定义为:
 (1)
(1)
其中, ;
; 且
且 为偶数,
为偶数, 。
。
1.1.2. Zernike矩的正交性
Zernike多项式
 (2)
(2)
是基于单位圆 上正交的一组完整复值函数,它满足以下条件,有
上正交的一组完整复值函数,它满足以下条件,有
 (3)
(3)
实值径向多项式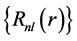 满足
满足
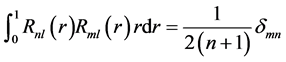 (4)
(4)
它被定义为
 (5)
(5)
1.1.3. Zernike矩的旋转不变性:
根据Zernike矩的定义式,如果图像 发生旋转,旋转角度为
发生旋转,旋转角度为 ,其旋转后的图
,其旋转后的图
像为 ,其n阶l重的Zernike矩为:
,其n阶l重的Zernike矩为:
 (6)
(6)
对上式做坐标代换,则有:
 (7)
(7)
由上式可以看出,基于Zernike矩可以构建旋转不变量,有
 (8)
(8)
由于图像旋转时候模值保持不变,因此对Zernike矩取模可以构建旋转不变特征,即Zernike矩具有旋转不变性。
1.1.4. 用迭代的方法计算Zernike多项式 [20]
实值径向多项式的递归关系式为:
 (9)
(9)
其中3个系数定义如下:
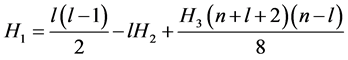 (10)
(10)
 (11)
(11)
 (12)
(12)
以上的关系式在n = l以及 时不成立,对于n = l,
时不成立,对于n = l,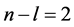 时满足以下关系式:
时满足以下关系式:
当n = l时
 (13)
(13)
当 时
时
 (14)
(14)
由上述关系时可以计算得出n阶l重的实值径向多项式,进而计算出Zernike多项式以及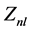 的值,提取出来的Zernike矩特征是一个向量,向量的列数就是n和l的组合数。
的值,提取出来的Zernike矩特征是一个向量,向量的列数就是n和l的组合数。
用迭代方法可以单独求得任意阶矩的极径多项式,相比于Direct、Belkasim、Prata、Kintenr以及Coefficient方法,迭代计算过程中的乘法次数少,计算时间快,因此本实验采用这种方法计算Zernike多项式,进而提取Zernike矩特征。
1.2. kNN算法
1.2.1. 算法介绍
k近邻分类算法是一种最简单的机器学习算法。它采用测量不同特征值之间的距离方法进行分类。它的思想很简单:如果一个样本在特征空间中的k个最相似的样本中的大多数属于某一个类别,则该样本也属于这个类别。
1.2.2. 算法具体内容
k近邻算法的计算步骤如下: 1) 算距离:给定测试对象,计算它与训练集中的每个对象的距离。
2) 找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻。
3) 做分类:根据这k个近邻归属的主要类别,来对测试对象分类。
kNN算法的分类效果与k值的选取有关,k太小,分类结果易受噪声点影响。k太大,近邻中又可能包含太多的其它类别的点,根据经验k值一般低于训练样本数的平方根。文中所使用的kNN算法的k值为1,即找出测试集中每张图像与训练集中所有图像中欧氏距离最小的值,看该图像属于训练集中的哪一类,由此实现极光图像的检测。
2. 极光图像检测
早期的极光检测工作主要是依据专家的经验进行人工标记,这种方法耗费大量的时间,而且主观性比较强。更主要的是近年来随着捕获的极光图像的数量的迅速增加,原始的人工标记的方法已经不能满足海量数据的处理的需求,所以有必要研究一种快速有效的自动检测极光图像的方法。
LBP是一种常见的基于图像纹理特征的特征提取的方法,用在极光的检测上也取得了不错的效果,但是,当图像混有的噪声比较严重、旋转了某个角度或者是先进行滤波处理,再利用LBP提取特征进行分类时,效果会明显下降,而文中提出的基于Zernike矩的极光图像检测算法不但具有很好的鲁棒性和旋转不变性,在滤波处理后也取得了较好的效果。
2.1. 极光图像检测算法
实验中整体上分为两大类,训练集和测试集。训练集和测试集中均包括有极光的图像和无极光的图像。其中训练集共有1000张图像,包含有500张有极光图像和500张无极光图像。测试集共有2000张图像,包含有1000张有极光图像和1000张无极光图像。本实验采用128 × 128的图像进行极光图像检测,其算法的步骤如下:
1) 对训练集提取特征:对训练集中的1000张图像提取Zernike特征。
2) 对测试集提取特征:对测试集中所有图像分别添加均值为零,方差不等高斯噪声、感染密度不同的椒盐噪声、旋转不同的角度、用不同的窗口大小进行平滑滤波,然后对其提取Zernike特征。
3) 计算相似性度量:分别计算测试集中每张图像与训练集中所有图像之间的欧氏距离,用于度量不同图像之间的相似程度。
4) kNN分类:找出最小的k个距离,k一般为奇数值,然后根据k中大多数属于的类别来确定测试集中该对象所属的类别,进而完成极光的检测。
Zernike矩特征向量的提取过程中涉及到阶数n的选择,实验表明:对大小为128 ´ 128的极光图像提取Zernike矩,当n = 15时,Zernike矩的分类效果达到最好。
2.2. 实验结果与分析
实验过程中,首先对训练集和测试集中所有图片提取LBP特征向量以及Zernike特征向量,然后求得测试集中每张图像与训练集中所有图像的欧氏距离,再利用kNN算法进行分类,在kNN算法中,取k的值为1。之后分别对测试集中的图像添加噪声、旋转以及平滑滤波,再对比两种特征提取方法的分类效果,实验结果如下。
2.2.1. 加噪
1) 椒盐噪声
首先对训练集中的图像分别提取LBP特征向量,以及Zernike矩的特征向量,再对测试集中每张图像添加不同感染密度的椒盐噪声,之后提取其LBP以及Zernike矩的特征向量,然后利用提取出来的特征计算测试集中每张图像与训练集中所有图像的特征向量的欧氏距离,最后利用kNN算法中k = 1的值进行分类,实验结果如图1所示。
实验表明:在没有添加椒盐噪声之前,LBP的分类效果接近100%,Zernike矩的分类效果为95.25%。添加椒盐噪声之后,LBP特征提取的分类效果随着感染密度的增大迅速下降,而Zernike矩特征提取的分类效果下降缓慢。由此可见,在对图像添加椒盐噪声后,Zernike矩的分类效果更好。
2) 高斯噪声
首先对训练集中的图像分别提取LBP特征向量,以及Zernike矩的特征向量,再对测试集中每张图像添加均值为0,方差不同的高斯噪声,之后提取其LBP以及Zernike矩的特征向量,然后利用提取出来的特征计算测试集中每张图像与训练集中所有图像的特征向量的欧氏距离,最后利用kNN算法中k = 1的值进行分类,实验结果如图2所示。
从实验结果可以看出,在没有添加高斯噪声之前,LBP的分类效果接近100%,Zernike矩的分类效果为95.25%。添加高斯噪声之后,LBP的分类效果迅速下降为50%,而Zernike矩的分类效果变化幅度不是很大。
程序运行的结果显示,添加高斯噪声之后,用LBP特征提取的方法对测试集分类时50%的错误率大部分是无极光图片发生了错误,为了说明实验结果的正确性,分别从训练集中的有极光和无极光的图像中选取了n张具有典型代表的图像,提取这些图像的LBP特征向量并画出直方图,之后再从测试集中的
有极光和无极光的图像中选取相同数量的具有典型代表的图像,对它们添加高斯噪声之后再次提取其LBP特征向量并画出直方图,得到的直方图如图3、图4、图5所示。
 (a) (b)
(a) (b)
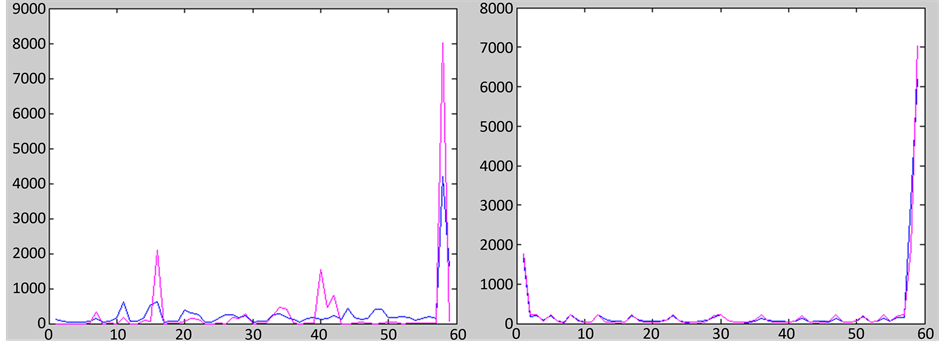
Figure 3. (a) LBP histogram of training set with n = 1; (b) LBP histogram after adding noise to test set when n = 1
图3. (a) n = 1时训练集的LBP直方图;(b) n = 1时测试集加噪后的LBP直方图
 (a) (b)
(a) (b)
Figure 4. (a) LBP histogram of training set with n = 20; (b) LBP histogram after adding noise to test set when n = 20
图4. (a) n = 20时训练集的LBP直方图;(b) n = 20时测试集加噪后的LBP直方图
 (a) (b)
(a) (b)
Figure 5. (a) LBP histogram of training set with n = 100; (b) LBP histogram after adding noise to test set when n = 100
图5. (a) n = 100时训练集的LBP直方图;(b) n = 100时测试集加噪后的LBP直方图
由上图可知,训练集中未经处理的有极光和无极光图片的LBP直方图相差挺大,但是测试集中加噪之后的有极光和无极光图片的LBP直方图十分接近,正是由于这个原因,使得测试集经过加噪之后,有极光和无极光的图片都被分到了同一个类别,才会出现接近于50%的分类正确率。
2.2.2. 旋转
首先对训练集中的图像分别提取LBP特征向量,以及Zernike矩的特征向量,再对测试集中每张图像旋转不同的角度,之后提取其LBP以及Zernike矩的特征向量,然后利用提取出来的特征计算测试集中每张图像与训练集中所有图像的特征向量的欧氏距离,最后利用kNN算法中k = 1的值进行分类,实验结果如图6所示。
实验表明:在没有旋转之前,LBP的分类效果接近100%,而Zernike矩的分类效果为95.25%。经计算可得,旋转之后LBP分类效果的平均值为83.91%,而Zernike矩分类效果的平均值为95.23%,由此可见,在对图像进行旋转之后,Zernike矩的检测效果更好。
2.2.3. 平滑滤波
首先对训练集中的图像分别提取LBP特征向量,以及Zernike矩的特征向量,再对测试集中每张图像加窗口大小不同的滤波器进行平滑滤波,之后提取其LBP以及Zernike矩的特征向量,然后利用提取出来的特征计算测试集中每张图像与训练集中所有图像的特征向量的欧氏距离,最后利用kNN算法中k = 1的值进行分类,实验结果如图7所示。
3. 结束语
通过对极光图像进行提取特征,找到了一种比传统的LBP特征提取效果更好的一种方法,即Zernike矩特征的方法。它具有抗噪性强、具有旋转不变性并且在图像经过平滑滤波后依然能保持良好的分类效果。
致谢
在研究生学习期间,由于刚刚接触算法这一类问题,很多东西不知道从哪里下手去做,这段期间得到了王晅老师的耐心指导,并会时常鼓励我们,在实验室也从李志权、杨腾飞师兄、时光慧师姐以及曹振婷他们那里学到了很多知识,在此表示深深地感谢!
此外还要感谢物理学与信息学院的带课老师,感谢辛云宏、郭建中、李锦、曹辉以及陈春娥老师,是他们让我学到了很多专业的知识,为研究生的学习打下了基础,在此表示感谢。