1. 引言
记忆(memory)是人们积累和保存个体经验的过程。作为一种加工过程,记忆是指存储和提取过去经验的一种动态机制(Olson, Moore, Stark et al., 2006)。
长时记忆(Long-term memory, LTM)是相对于感觉记忆和短时记忆而言的,指存储时间在一分钟以上,最长可以保持终生的记忆。它存储着我们过去的经验和知识,为所有心理活动提供必要的知识基础。长时记忆的信息存储时间比较长,容量几乎是无限的。长时记忆的提取是指当有需要时,大脑会将有关信息从长时记忆中调出,放到工作记忆中以供使用,有回忆和再认两种提取形式。这两种形式提取信息都需要运用一定的策略,即依靠一定的线索或选择一定的中介。
对长时记忆信息进行提取,可能是选择性检索已有的记忆内容,也可能是由于某种需要而对提取的部分信息进行抑制。Bunting等人(2004)认为低工作记忆容量个体对干扰更敏感(Bunting et al., 2004)。Anderson和Spellman (1995)认为记忆提取过程涉及以往学习过的与当前目标相关的信息,也涉及学习过但与当前提取目标无关的信息,后者对前者显然有干扰作用,而提取过程必须克服这种干扰,用于克服这种竞争性干扰项目的机制就是一种抑制机制,叫提取抑制(Anderson & Spellman, 1995)。
对长时记忆进行研究主要有两种方法:回忆任务和再认任务。回忆任务(包括自由回忆、序列回忆和线索回忆)中,给被试呈现一系列的TBR (to-be-remembered)项目,短暂延迟后要求被试尽可能回忆出之前呈现的项目。再认任务中先给被试呈现一系列的TBR项目,然后在测试阶段呈现一个项目,要求被试判断该项目是否有在之前出现过(Unsworth, 2010)。
工作记忆(working memory)是指个体在执行认知任务过程中,对信息暂时储存加工的有限的资源系统(Baddeley & Hitch, 1974)。工作记忆被形容为人类的认知中枢,在高级认知活动中具有双重作用:一方面保存从长时记忆中提取的信息,另一方面暂时存储外界输入的信息。从信息加工过程来看,Smith和Jonides提出(Smith & Jonides, 1998),工作记忆系统中的信息加工可分为三个环节:编码(encoding)过程,学习并获取信息,但是信息很容易消退;信息保持或复述过程(retention or rehearsal),通过不断复述来激活贮存器中正在消退的信息;执行加工过程(execute),负责信息加工过程的控制、协调与信息的执行和提取。
长时记忆与工作记忆之间的关系如何呢?有学者认为长时记忆和工作记忆是完全独立的,也有学者认为长时记忆与工作记忆是单一的记忆系统,更有人认为二者是嵌套关系。
2. 长时记忆与言语工作记忆的关系
2.1. 长时记忆与工作记忆完全独立
早期关于工作记忆和长时记忆的理论表明,两种记忆结构的表征有着质的不同,是独立的记忆系统。工作记忆在一个相对较短的时间内负责保持和操作少量的信息,而长时记忆负责保存一个人在生活中所获得的所有的记忆信息。这两个系统代表了记忆的不同功能,两者具有不同的性质,而且神经基础和遗忘机制也是不同的,两者是彼此独立的,这种观点得到行为、神经心理学和神经影像学的支持。神经心理学方面方面有大量的研究支持长时记忆与工作记忆的分离,结论大致如下:内侧颞叶包括海马在内的内侧颞叶系统受损的病人长时记忆亏损(Cave & Squire, 1992),但短时记忆完好(Scoville & Milner, 1957);而颞叶的其他区域如TE区则与知觉和短时记忆有较大关联。外侧颞周区受损的病人短时记忆的语音信息功能受损,但长时记忆完好(Shallice & Warrington, 1970);颞下皮层可能存储着长时记忆的视觉刺激表象(Gross, 1972);额叶皮层可能是短时记忆的存储区(Funahashi, Bruce, & Goldman-Rakic, 1989)。
2.2. 长时记忆与工作记忆是单一的记忆系统
另一些理论认为长时记忆与工作记忆是单一的记忆系统,在这个系统中既可以操作短时记忆也可以操作长时记忆,工作记忆任务和长时记忆任务中存在同样的效应,它们似乎追寻相似的规则,而且单一的记忆系统会更节俭,既可以记忆短时记忆的东西也可以记忆长时记忆的东西,因此并没有必要将两者区分开来(Crowder, 1982)。
Nairne’s的特征模型(1990)是一个单一的记忆模型,这个模型可以成功解释许多传统的工作记忆效应;Brown,Preece,和Hulme (2000)的OSCAR模型可以成功的解释以往用来支持工作记忆的系列顺序效应;Brown,Neath,和Chater’s SIMPLE模型(2007)也可以解释大量的效应,包括自由回忆中的系列位置效应,而这种效应长期被认为是分离工作记忆和长时记忆的证据。因此,这种明确的单一记忆模型可以用单个框架解释很多工作记忆和长时记忆的效应。
2.3. 嵌套关系
20世纪以来,有研究表明(Fleteher & Fleteher, 200l; D’Esposito, 1999)工作记忆和长时记忆的脑区激活具有重叠性,主要是在前额皮层。持此种观点的研究者认为短时记忆(工作记忆)和长时记忆会有相同的实验效应,而且它们的神经基础应该是有重复的,两者应该是既相互独立又有重叠的。
Ranganath & Blumenfeld (2005)指出短时记忆和长时记忆的不同程度的激活大脑皮层存储器从而导致其神经机制的分离。长时记忆和短时记忆是外界的刺激或者是记忆提取的信息对大脑皮层记忆网络的重新激活,大脑皮层记忆存储区的关键不同不是因为记忆不同的保持时间,而是信息加工和表征的形式。
Botvinick (2001)采用2-back工作记忆范式和长时记忆编码有意记住、yes-no提取再认任务,运用熟悉单词和不熟悉面孔两种不同类型的材料,考察任务类型与材料类型的不同影响,结果发现,执行工作记忆和长时记忆形成任务时,前额叶腹外侧都被激活,但是前额叶外侧和前部在工作记忆任务中有选择行的被激活。这说明在工作记忆和长时记忆任务中两者具有共同的激活区,那么这种脑区的重合可能反映了长时记忆任务中工作记忆的作用,也可能是工作记忆任务中长时记忆的作用。
而且有研究发现工作记忆延迟阶段脑区激活与该刺激的长时记忆表征高度一致。面孔刺激在工作记忆延迟阶段激活了颞下皮层区,同时颞下皮层区也负责对面孔的长时保存(Druzgal & D’Esposito, 2003; Ranganath, DeGutis, & D’Esposito, 2004)。Lewis-peacock & Postle采用FMRI技术探讨了工作记忆是长时记忆的激活。在实验中长时记忆是让判定对3类不同图片的喜欢程度,工作记忆任务则是让被试对之前的图片进行延迟匹配再认,实验记录了长时记忆任务中和工作记忆延迟阶段的的激活脑区,结果发现,工作记忆延迟阶段的脑区激活与长时记忆任务中的脑区激活有重叠,证明了长时记忆的激活表征有利于工作记忆任务的完成。
2.4. 问题提出
那么长时记忆对工作记忆容量到底存在什么样的影响呢?Saito (2000)发现真词的记忆成绩要好于非词,呈现出词汇效应,类似单词的非词记忆成绩好于非类似单词的非词记忆成绩,呈现出近似单词效应,这两种效应都在一定程度上说明长时记忆中的词汇信息对语音回路的功能有显著的影响(Saito, 2000)。近年来某些研究者利用FMRI技术探讨了长时记忆中已有的知识经验对工作记忆的影响,Jiang等的研究表明,对于事先经过学习且已在长时记忆中贮存的客体,在完成不同的工作记忆任务时,同等熟悉的物体既可以激起增强的神经反应也可以激起衰减的神经反应。大脑前额皮层在靶项目和干扰项目的区分方面起着重要的作用,工作记忆中增强和衰减的神经机制共同参与,使得工作记忆任务更有效的完成。
本论文欲在以往研究的基础上,提出以下问题:长时记忆对工作记忆容量有什么样的影响?我们预通过实验1:采用3 × 3 (手机模板数字固定、手机模板数字随机、无模板三种刺激呈现方式) × 呈现数目(4, 6, 8)被试内设计来解决此问题,无模板设为基线条件。我们预测手机固定模板数字固定的成绩会高于基线,基线高于手机模板数字随机,而且随着记忆容量的增大这种差异会变大;而且手机模板数字随机这种条件会对工作记忆产生干扰作用。
3. 实验——长时记忆对言语工作记忆容量的影响
本实验主要解决问题:长时记忆信息是否可以使工作记忆的容量增大?在材料选取上我们选择了日常生活中常用的手机模板。手机模板数字固定的成绩受到长时记忆、空间布局的影响,假设两者会同时促进言语工作记忆任务;手机模板数字随机的成绩受到空间布局的影响,促进言语工作记忆任务,同时会受到与长时记忆冲突的影响,削减言语工作记忆成绩;手机模板符号随机只受到空间布局的影响,设为基线条件。如果手机模板数字固定的成绩高于手机模板数字随机,则说明长时记忆促进了言语工作记忆成绩。
3.1. 实验前测
实验前测目的:探测被试的工作记忆成绩。
3.1.1. 被试
随机选取38名本科生和研究生(男生12人,女生26人),年龄在20~25岁之间,平均年龄23.5岁,裸视或矫正视力正常,均未参加过类似实验,自愿参加本实验,实验之后给予相应的报酬。
3.1.2. 实验设计
2 × 4混合设计,因素一为序列呈现的数目,分为5,6,7,8四个水平,为被试内变量;因素二为呈现的刺激,包括0~9的数字和10个符号(实验材料中详述),为被试间变量。因变量记录被试的正确率。
3.1.3. 仪器与材料
实验程序采用E-Prime2.0进行编程。实验在微亮的单间隔音实验室里进行,刺激呈现在IBM Pentium IV型计算机的17寸液晶显视器上,屏幕背景为银灰色(下同)。
实验材料包括0~9的十个数字,· (点),+ (加),- (减),× (乘),÷ (除),← (左),↑ (上),→ (右),↓ (下),○ (圆)十个符号,均为Arial22号字体,放在边长为39像素,颜色为绿色的正方形方格中。
3.1.4. 实验程序
本实验主要采用序列呈现范式。实验前先让符号组被试正式学习符号材料,主试检查编码无误后开始进行实验。
首先在屏幕中心呈现注视点“+”1000 ms,然后屏幕中央序列呈现记忆目标,每个记忆目标呈现时间为500 ms,每两个目标间会有500 ms的灰屏掩蔽,每个试次中的记忆目标不会重复,呈现完成后会在屏幕上出现“请按顺序回忆”,要求被试按顺序输入刚才呈现的目标,记录被试的正确率(提前在键盘上贴上符号)。反应完1000 ms之后自动进入下一次试验。
实验中4种呈现数目随机出现,每种条件有24次试验,每个被试共需完成96次试验,正式实验之前有至少12次练习,直至完全掌握实验的操作。
3.2. 实验1——长时记忆对工作记忆成绩的影响
实验目的:探讨长时记忆对工作记忆成绩的影响。
3.2.1. 被试
与前测阶段采用同一批被试。
3.2.2. 实验设计
本实验采用3 × 4两因素混合设计。因素一为刺激呈现方式,有3个水平:手机模板数字固定、手机模板数字随机、手机模板符号随机,为被试间变量;因素二为序列刺激集合大小,有4种水平:序列呈现5个目标,序列呈现6个目标,序列呈现7个目标,序列呈现8个目标,为被试内变量。因变量为序列回忆的正确率。
3.2.3. 实验材料
实验材料如图1所示,包括手机模板数字固定、手机模板数字随机、手机模板符号随机三种材料。
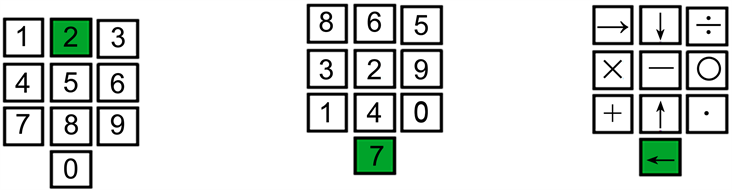
Figure 1. Three different cell phone template materials
图1. 三种不同手机模板材料
1) 手机模板数字固定
注视点1000 ms后,屏幕中央会出现一个手机键盘(长557像素,宽113像素),0~9 (Arial22号字体)这10个数字按正常顺序分布在键盘上。500 ms后手机模板上会随机出现一个数字变绿,呈现时间为500 ms,被试要记住这个数字,接着呈现500 ms掩蔽,然后再随机有一个数字变绿500 ms,按照这种方式一直呈现完5个(或6,7,8个)数字,最后呈现“请按顺序回忆”,要求被试按顺序回忆刚才变绿的数字并输入,记录被试的正确率。
2) 手机模板数字随机
注视点1000 ms后,屏幕中央会出现一个手机键盘(长557像素,宽113像素),0~9 (Arial22号字体)这10个数字在键盘上随机排列。500 ms后手机模板上会随机出现一个数字变绿,呈现时间为500 ms,被试要记住这个数字,接着呈现500 ms掩蔽,然后再随机有一个数字变绿500 ms,按照这种方式一直呈现完5个(或6,7,8个)数字,最后呈现“请按顺序回忆”,要求被试按顺序回忆刚才变绿的数字并输入,记录被试的正确率。
3) 手机模板符号随机
程序同手机模板数字随机,只是键盘上出现的是“·,+,-,×,÷,←,↑,→,↓,○”10个符号,随机排列在键盘上。
3.2.4. 实验程序
实验中4种序列刺激集合随机出现,每种条件有24次试验,每个被试共需完成96次试验,正式实验之前有至少12次练习,直至完全掌握实验的操作。
3.2.5. 结果与分析
本论文的数据均通过SPSS 16.0统计软件包进行处理。本实验主要采用正确率作为因变量进行分析。实验1a的正确率平均数和标准差如表1所示。

Table 1. Accuracy rate of different number of targets presented by sequence under three presentation modes (M ± SD)
表1. 序列呈现不同数目的目标在三种呈现方式下的正确率(M ± SD)
4 × 3混合设计方差分析表明,不同呈现方式主效应显著,F(2, 35) = 40.34,p < 0.01,事后检验表明,ACC固定 > ACC符号(p < 0.01),ACC随机 > ACC符号(p < 0.01)。由以上统计结果可以发现符号任务难度大于数字任务,作为基线并不合适,所以在以下的统计结果中将其删除。进行4 × 2混合方差分析,结果表明,同时呈现数目主效应显著,F(3, 105) = 41.31,p < 0.01,ACC5 > ACC6 > ACC7 > ACC8,同时呈现数目与呈现方式交互作用显著,F(6, 105) = 3.16,p < 0.05。为了揭示交互作用的实质,我们进一步进行了简单效应分析。结果发现在同时呈现7个项目时,手机固定数字和手机随机数字差异边缘显著,F(1, 27) = 3.98,p = 0.056。通过图2我们可以直观地看出序列刺激数目与呈现方式的这种交互作用。

Figure 2. The accuracy rate of fixed number and random number in different rendering numbers
图2. 固定数字和随机数字在不同呈现数目下的正确率
通过上述结果分析,似乎在同时呈现数目为7时手机模板数字固定对工作记忆产生促进作用,为了更清楚的了解手机模板是否对工作记忆产生了影响,我们将固定和随机条件下每个被试在实验1 (有模板)中的正确率减去前测(无模板)中的正确率,进行2 × 4混合方差分析,结果表2:序列刺激数目与呈现方式的交互作用显著,F(6, 102) = 2.84,p < 0.05。

Table 2. Accuracy difference of three groups of subjects with or without template (M ± SD)
表2. 三组被试有无模板条件下的正确率之差(M ± SD)
在序列刺激项目的不同水平下,我们对两种呈现方式进行了简单效应分析,结果发现,当同时呈现7个项目时,固定条件和随机条件差异边缘显著,F(1, 27) = 4.06,p = 0.054。图3可以让我们更直观的看出这种交互作用。

Figure 3. Accuracy difference of three groups of subjects with or without template
图3. 三组被试有无模板的正确率之差
3.2.6. 分析与讨论
通过上述统计结果发现当同时呈现7个项目时,手机模板数字固定的正确率大于手机模板数字随机,而且差异边缘显著,初步证实了实验假设。按照此种逻辑推理应该是同时呈现的数目越多,长时记忆的促进作用越明显,但是没有发现这种效应。分析原因可能是因为实验材料过于粗糙,手机模板的形象性太差,为此我们在实验2中进行了改进。而且这种差异有可能是长时记忆对工作记忆的促进产生的,也可能是抑制作用产生的,或者是两者共同作用,这需要再接下来的实验中进一步探讨。通过实验1发现基线选择不恰当,符号的记忆任务比数字难,所以在实验2中我们重新选择了模板。
3.3. 实验2——长时记忆对言语工作记忆的影响
实验目的:探讨实验1中出现的固定与随机的差异是由于长时记忆的促进产生的还是由于抑制产生的或者两者同时发挥了作用?
3.3.1. 被试
随机选取18名本科生和研究生(男生6人,女生12人),年龄在19~24岁之间,平均年龄22.3岁,裸视或矫正视力正常,均未参加过类似实验,自愿参加本实验,实验之后给予相应的报酬。
3.3.2. 实验设计
3 × 3被试内设计,因素一为同时呈现数目,分为4,6,8三个水平;因素二为刺激呈现方式,包括手机模板数字固定、手机模板数字随机和无模板三个水平。因变量记录被试的正确率和反应时。
3.3.3. 仪器和材料
本实验的仪器和编程软件与实验1相同。实验中使用的手机模板大小为237 × 494像素。0~9的十个数字均为Arial22号字体,图片大小为59 × 37像素。
3.3.4. 实验程序
本实验主要采用延迟匹配范式。根据实验任务的要求分3个Block进行。
1) 手机模板数字固定
首先在屏幕中心呈现注视点“+”500 ms,然后屏幕中央呈现手机模板,键盘上会随机出现4个(或6个,8个) 0~9的不重复数字,这些数字出现在键盘的正确位置上,500 ms后会有900 ms的灰屏掩蔽,之后会在屏幕中央再次出现手机模板,上面只有一个数字,且出现在正确的位置上,被试的任务是判断该数字是否有在之前出现过,如果是按“F”键,否则按“J”键。
2) 手机模板数字随机
首先在屏幕中心呈现注视点“+”500 ms,然后屏幕中央呈现手机模板,键盘上会随机出现4个(或6个,8个) 0~9的不重复数字,这些数字在键盘上的位置是随机的,500 ms后会有900 ms的灰屏掩蔽,之后会在屏幕中央再次出现手机模板,上面只有一个数字,且位置是随机的,被试的任务是判断该数字是否有在之前出现过,如果是按“F”键,否则按“J”键。
3) 无模板
首先在屏幕中心呈现注视点“+”500 ms,然后屏幕上会随机出现4个(或6个,8个) 0~9的不重复数字(出现的位置与有模板条件下匹配),这些数字的排列顺序是随机的,500 ms后会有900 ms的灰屏掩蔽,之后会在屏幕中央出现一个数字,被试的任务是判断该数字是否有在之前出现过,如果是按“F”键,否则按“J”键。
根据刺激呈现方式的不同,实验分三个Block进行,采用被试间拉丁方顺序进行平衡。每个Block都先进行练习,直到被试完全理解实验要求并且正确率达到80%以上进入正式实验。每个Block中有四种刺激数目条件,每个条件有30次试验,这些试验中均有一半的反应为“是”,一半的反应为“否”。在每两个Block之间休息1分钟。
3.3.5. 结果与分析
1)正确率分析
同时呈现不同数目刺激在三种呈现方式下的正确率成绩如表3所示。以刺激呈现数目和呈现方式为自变量的3 × 3被试内方差分析表明,同时呈现数目主效应显著,F(2, 34) = 96.1,p < 0.01。事后检验表明,其正确率的排列顺序为:ACC4 > ACC6 > ACC8。不同呈现方式主效应显著,F(2, 34) = 14.11,p < 0.01.事后检验表明,其正确率的排列顺序为:ACC固定 > ACC随机 > ACC无模板。同时呈现数目与不同呈现方式交互作用显著,F(4, 68) = 6.36,p < 0.01。为了更好的揭示这种交互作用的实质,进行了简单效应检验。

Table 3. Accuracy rate of presenting different number of stimuli simultaneously under different presentation modes (M ± SD)
表3. 不同呈现方式下同时呈现不同数目刺激的正确率(M ± SD)
呈现方式在呈现数目三个水平上的简单效应检验表明,同时呈现6个时三种呈现方式差异显著,F(2, 34) = 19.6,p < 0.01,固定数字组和随机数字组的正确率均高于无模板组;同时呈现8个数字时,F(2, 34) = 7.66,p < 0.01,固定组的正确率高于随机数字组和基线组,随机组和无模板组差异不显著。但是我们可以发现同时呈现6个和8个数字时,随机组和无模板组的正确率差异变小,随机组的正确率下降的更快。可以通过图4直观的描述出来。
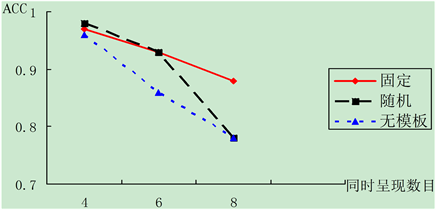
Figure 4. The accuracy of different rendering methods under different numerical conditions at the same time
图4. 不同呈现方式在同时呈现不同数字条件下的正确率
2) 反应时分析
同时呈现不同数目刺激在三种呈现方式下的反应时如表4所示。以刺激呈现数目和呈现方式为自变量的3 × 3被试内方差分析表明,同时呈现数目主效应显著F(2, 34) = 27.49,p < 0.01。事后检验表明,RT4 < RT6 < RT8 (p < 0.05)。呈现方式主效应显著,F(2, 34) = 22.06,p < 0.01,事后检验表明,RT固定 > RT随机 > RT基线(p < 0.01)。同时呈现数目与呈现方式交互作用显著,F(4, 68) = 2.78,p < 0.05。为了更好的揭示这种交互作用的实质,需要进行两个方向的简单效应检验。

Table 4. Accuracy rate of presenting different number of stimuli simultaneously under different presentation modes (M ± SD)
表4. 不同呈现方式下同时呈现不同数目刺激的反应时的正确率(M ± SD)
呈现方式在呈现数目三个水平上的简单效应检验表明,对三种呈现数目而言,三种呈现方式的简单效应均显著,同时呈现4个时,三种呈现方式差异显著,F(2, 34) = 21.4,p < 0.01,固定与随机差异显著F(1, 17) = 12.82,p < 0.01。固定与基线差异显著F(1, 17) = 29.07,p < 0.01,随机与基线差异显著F(1, 17) = 18.4,p < 0.01;同时呈现6个时,三种呈现方式差异显著,F(2, 34) = 8.01,p < 0.01,固定与基线差异显著F(1, 17) = 24.05,p < 0.01随机与基线差异显著F(1, 17) = 4.94,p < 0.01,同时呈现8个时,三种呈现方式差异显著,F(2, 34) = 12.69,p < 0.01。固定与基线差异显著F(1, 17) = 31.74,p < 0.01。随机与基线差异显著F(1, 17) = 8.93,p < 0.01。图5可以让我们更为直观的了解这种交互作用。

Figure 5. RT under different numerical conditions is presented in three ways at the same time
图5. 三种呈现方式在同时呈现不同数字条件下的RT
3.3.6. 分析与讨论
通过正确率的分析结果我们发现,同时呈现4个数字时,三种呈现方式的正确率差异不显著,4个数字在个人的记忆容量范围内,这个时候长时记忆不需要发挥作用。但是随着记忆数目的增加,当同时呈现6个数字时,固定模板和随机模板均高于无模板条件下,长时记忆已经开始发挥作用,固定数字模板的正确率显著高于基线,可以说这种正确率的提高是由长时记忆的促进作用产生的;而同时呈现6个数字时,随机数字模板的正确率也高于基线水平,可能是因为其抑制作用还没有表现出来(或者是其抑制作用还不足于抵消掉单纯的工作记忆);但是当同时呈现8个数字时,模板随机的正确率下降速度显著快于无模板组和模板固定组,这个时候模板随机数字与无模板组相比正确率已经持平,这种快速的下降速度可能是由于长时记忆的抑制作用产生的。
所以根据此正确率的结果分析我们可以得出以下结论:当同时呈现的数字超出被试的工作记忆容量范围时,手机模板固定数字对数字工作记忆存在促进作用,手机模板随机数字对数字工作记忆存在抑制作用。
通过反应时的分析我们可以发现固定数字的反应时始终大于基线和随机数字条件,那么为什么会出现这样的情况呢?我们猜测可能是因为长时记忆提取需要一定的时间。当长时记忆提取面临干扰时,不仅存在对目标信息的激活机制,也存在对干扰信息的主动抑制机制。并且在某些记忆提取任务中,提取过程是控制性的。
4. 讨论
本实验采用3 × 3被试内设计考察了长时记忆对工作记忆容量的影响。当同时呈现6个数字时,固定模板和随机模板的正确率均高于无模板条件下,固定数字模板的正确率显著高于基线;当同时呈现8个数字时,模板随机的正确率下降速度显著快于无模板组和模板固定组。固定模板的成绩受到长时记忆、空间布局的影响,假设两者会同时促进言语工作记忆任务;随机模板的成绩受到空间布局的影响,促进言语工作记忆任务,同时也可能会受到与长时记忆中信息冲突的影响,削减言语工作记忆成绩;而无模板只受到空间布局的影响,设为基线条件。根据此种实验逻辑以及实验结果我们可以说:当同时呈现的数字超出被试的工作记忆容量范围时,固定模板对言语工作记忆存在促进作用,模板随机对言语工作记忆存在抑制作用。这与Jiang等人的研究结果接近,他们利用FMRI技术探讨了长时记忆中已有的知识经验对工作记忆的影响,结果发现对于事先经过学习且已在长时记忆中贮存的客体,当赋予不同的工作记忆任务时,同等熟悉的物体既可以激起增强的神经反应也可以激起衰减的神经反应。而且通过对反应时的分析发现固定模板的RT大于随机模板和无模板条件下的RT,这提示我们长时记忆的提取需要一定的时间,通过数据分析发现,固定模板与基线的反应时差异为100 ms~200 ms之间,这与郭春彦等人的研究具有相似之处,他们对于青年人(18~28岁)的事件相关电位实验表明,贮存在长时记忆中的熟悉客体与新客体相比,两者同时为靶、或同时为分心物时的大脑神经机制具有差异,对新客体的加工比情景记忆中熟悉客体的加工提前50 ms (Guo et al., 2010)。
5. 结论
长时记忆对言语工作记忆容量有促进作用。当前的工作记忆任务超出被试的工作记忆容量范围时,长时记忆中的激活信息对工作记忆产生促进作用,而且长时记忆信息的提取需要一定的时间。
参考文献