1. 引言
分光光度法是一种简单而科学的分析方法,既可应用于无机领域又可应用于有机领域,既可测定微量组分又可测定高含量,并容易实现多组分的联测,节能减排 [1] [2]。但由于干扰因素多且复杂,掩盖了它的真实规律,致使人们长期坚守比尔定律,而把它与光度法实际的不符,归咎于入射光的非单色性 [3] [4] [5] [6] [7]。在无法获得单色入射光的情况下,实际工作采用多个标准绘制“校准曲线” [8] [9] [10] [11] [12],造成了光度法测定含量有限、实施程序繁杂、环境污染严重。实践证明,“精密度法则”,即“保持各影响因素对于同一测定系列各个样品影响的一致性”,可使各种影响因素对同一测定系列各个样品的干扰趋于一致,显示出光度法的真实规律,展现出它在分析化学中无可替代的功能。本文以钢铁中锰的测定为例,作详细介绍。
2. 实验部分
2.1. 主要仪器及试剂
分光光度计:721型,中国上海精密仪器仪表有限公司;硝酸溶液(体积比):硝酸:水 = 1:4;硫–磷混酸(体积比):硫酸:磷酸:水 = 1:1:2;过硫酸铵溶液(质量比):5%过硫酸铵水溶液(现用现配);硝酸银溶液(质量比):1%硝酸银水溶液,1000 ml加20 ml硝酸;实验用水必须是蒸馏水;试剂均为分析纯。
2.2. 实验方法
严格遵循“精密度法则”,同一测定系列,由同一人在同一天平称取试样0.2000 g置于200 ml锥形瓶,加硝酸溶液30 ml,加热溶解,赶去氮化物。取下,流水冷却至室温。由同一人用同一100 ml容量瓶加水定容,作为样品“母液”。由同一人用同一10 ml刻度移液管,移取10 ml“母液”置于200 ml锥形瓶。由同一人用同一5 ml刻度移液管,分别加入硝酸银溶液、过硫酸铵溶液各5 ml。在80℃~100℃水浴中摇动加热40 s,取出,流水冷却至室温。30 min内,由同一人用同一1 cm比色皿,以水作参比,在520 nm不变动条件下测定
吸光度。
3. 结果与讨论
3.1. “精密度法则”在光度法中的作用
实践证明,光度法测定中的人员、器械、物料、方法、环境都会严重影响它的测定结果,错乱光度法的真实规律。只有严格遵循“精密度法则”,即严格保持各干扰因素在同一测定系列各个样品(包括标准样品)的制备和测定中的同一性 [13],才能显现光度法的真实规律。同时,它是正态分布理论在光度法中的具体体现,使光度法的样本测得值近似正态分布,不仅易于发现系统误差和统计离群值,保证了测定结果的可靠性,而且简化了结果的不确定度评定,确立了不确定度的测量模型。
3.2. 化学物质吸光规律
选取多个碳钢标准样品,在严格遵循“精密度法则”条件下,按照本文2.2的方法,测定
的吸光度。测定结果列于表1。

Table 1. Absorption of manganese standard sample at 520 nm
表1. 锰标准样品520 nm的吸光度
根据表1数据,绘制锰的“校准曲线”(图1)。从图1可以看出,在入射光520 nm值域(0.10~0.86)内,所有样品的含量和吸光度的坐标点(C,A)都落在同一“校准曲线”上。曲线方程是“两点式”:
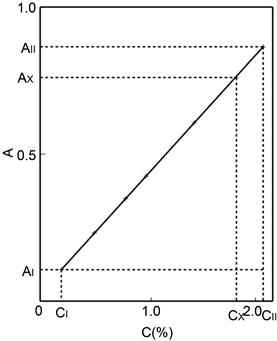
Figure 1. “Calibration curve” of Manganese
图1. 锰的“校准曲线”
(1)
从图1可知,曲线的方程可以有如下形式:
(2)
以吸光度改变量
、含量改变量
分别替代
和
,式(2)可简化为:
(3)
式(3)表明,“在入射光值域内,化学物质的吸光度改变量
与其相应的含量改变量
成正比:
”。我们称它为“化学物质吸光规律”。
“化学物质吸光规律”的存在,决定了入射光值域上、下限两个标准样品的坐标点连接线,即可作为样品含量的“测定线”,从而确立了“两标准光度法”,无需采用多个标准样品绘制“校准曲线”,因为“测定线”和“校准曲线”处于同一
的直线上。吸光度Ax对应的样品含量Cx,既可从“测定线”上查得,也可根据如下公式获得:
(4)
比如,样品Ax = 0.428的相应含量,从“测定线”上查得是0.96%,将Ax = 0.428、AI = 0.114、CII = 2.02%、CI = 0.19%、AII = 0.860代入式(4),得到的含量同样是0.96%:
上述事实表明“测定线”与式(4)是等效的,它们都是“化学物质吸光规律”的具体体现。但“校准曲线”(“测定线”)却与比尔定律不符,比如,“测定线”上吸光度Ax = 0.428的相应含量是0.96%,而按照比尔定律,若以含量0.19%、吸光度0.114作标准,则Ax = 0.428的相应含量为0.71%;若以0.77%、吸光度0.350作标准,则其含量为0.94%;若以1.40%、吸光度0.608作标准,则其含量又为0.99%;若以2.02%、吸光度0.860作标准,又成为1.01%。可见,按照比尔定律,只有用含量与样品逼近的标准样品进行换算,如0.77%或1.40%,才可得到较为接近样品实际含量的结果,而以与样品含量相差较大的标准换算,则两者含量相差越大,得到样品结果的系统误差误差也越大,这是采用比尔定律造成测定结果带有系统误差的根本原因(见本文3.4中的实例)。所以,认为光度法在“校准曲线”范围内符合比尔定律的观点仍然是错误的。
“化学物质吸光规律”不仅使光度法的实际操作得以简化,更重要的是,它奠定了光度法测定各种含量的理论基础,因为
中的含量改变量
,既可是痕量的改变量,也可是高含量的改变量。
3.3. “精密度法则”是正态分布理论在光度法中的具体体现
中心极限定理表明,如果受一系列独立因素影响的随机变量Xi的变化,对其总和的影响“都很微小”,则Xi的分布极限是正态分布 [14] [15]。也就是当
时,量值μ样本的测得值Xi是正态分布。尽管影响光度法的“人员、器械、物料、方法、环境”等因素千差万别,但只要在量值μ样本的各个观察值Xi的制备和测试过程,都严格遵循“精密度法则”,则各个观察值Xi就会“如出一模”,它们各自的变化对其总和的影响就必然“都很微小”,所以它们的“大样本(
)”就是正态分布。统计学又证明这时,n > 5的“小样本”近似正态分布,而且容量越大越近似正态分布 [16]。
3.4. “小样本”中系统误差的排除
实践证明,由于采用标准样品与被测样品含量的差异,按照比尔定律求得结果,常常含有系统误差。比如碳钢中锰的9个重复测定结果(%):0.68、0.69、0.68、0.67、0.69、0.71、0.72、0.69、0.70,就含有系统误差。因为遵循“精密度法则”的样本测得值近似正态分布,也就是测得值以均值为中心近似均称分布。比如,表2“两标准光度法”锰、硅、磷的10个测得值 [17],它们的分布都基本均称。而上述9个测得值,6个≥0.69,3个<0.69,分布明显不均称,表明有系统误差。根据“两标准光度法”会消除系统误差的事实,采用“两标准光度法”对其重新确定(%):0.66、0.66、0.67、0.66、0.67、0.66、0.68、0.67、0.73,其中≥0.67的是5个,<0.67的是4个,基本均称。实践证明,不经过系统误差排除,测定结果常常会是错误的 [18],本例排除前均值为0.69%,排除后为0.67%,两者显然不同。
3.5. “小样本”中统计离群值的排除
“小样本”测得值中常常存在异常数据,即统计离群值,它们会严重影响结果的可靠性。“小样本”近似正态分布,为发现统计离群值提供了条件。因为正态分布的样本均值
,会因测得值的不同而在极差中心的左右摆动,所以含最大残差ER的测得值,必然处于极差R与0.5R之间。我们采用“折半法”,在n = 5~10的“小样本”中,对其测得值进行选择,使超出(
)的测得值,即为GB/T4883-2008中格拉布斯法的“统计离群值” [19]。经过大量统计归纳,我们确定ER = 0.65R,即超出(
)的测得值,就是应剔除的统计离群值。上述3.4中不含系统误差的9个测得值(%):0.66、0.66、0.67、0.66、0.67、0.66、0.68、0.67、0.73,
= 0.67%,R = 0.07%。它们的(
)区间:0.62%~0.72%,测得值0.73%超出了该区间,所以是个应当剔除的统计离群值。清除0.73%后
= 0.67%既不含系统误差,也不含统计离群值,所以是可靠的。虽然清除0.73%前后的均值依然是0.67%,这并不表明这一清除没有必要,因为清除前的极差R = 0.07%,清除后的极差R = 0.02%。前者U95 = 0.02%,测定结果为(0.67 ± 0.02)%,kp = 2;后者U95 = 0.01%,测定结果为(0.67 ± 0.01)%,kp = 2。两个结果的不确定度差了一倍,表明只有排除了系统误差和统计离群值的结果才是真实可靠的。比如表2中“两标准光度法”锰、硅、磷的测得值,既排除了系统误差,同时又排除了统计离群值,所以它们才是真实可靠的 [17]。

Table 2. Determination results of “two standard photometry” for manganese, silicon and phosphorus
表2. 锰、硅、磷“两标准光度法”的测定结果
实践证明,以(
)判断统计离群值是必要的,也是有效的。它简化了格拉布斯法的应用,对于保证检测结果的可靠性是极为实用的。
3.6. “增量光度法”的确立
基于系统误差可改变“两标准光度法”的吸光度而不改变其样品含量的事实,我们确立了微含量样品测定的“增量光度法”。比如,应用
光度法对含锰量低于0.10%的铁粉样品X中锰的测定:选取含锰0.00%的纯铁粉B1和含锰量0.96%的碳钢B2,作为铁粉样品X锰测定的上、下限两个标准样品,并以含锰量0.96%的碳钢B2作为锰测定系列的系统“增量”,实施铁粉样品X中锰的测定。
按照本文2.2方法称取试样0.2000 g,制成各试样的“母液”100 ml。用同一10 ml刻度移液管分别移取各“母液”10 ml,分别置于3个200 ml的锥形瓶中。再用同一10 ml刻度移液管,向3个锥形瓶中分别加入B2“母液”10 ml作为测定系列的系统“增量”。再用同一5 ml刻度移液管向3个锥形瓶中分别加入硝酸银溶液、过硫酸铵溶液各5 ml。然后按照本文2.2方法显色、测定各自
的吸光度。
铁粉X、纯铁粉B1、碳钢B2三个样品的吸光度分别为0.310、0.300、0.560。纯铁粉B1锰含量为0.00%,标准B2在体积20 ml时锰含量为0.96%,在体积为30 ml时锰含量则为0.64%。以B1、B2两个的坐标点(0.00%,0.300)、(0.64%,0.560)连接线作为样品X锰的“测定线”,查得铁粉X吸光度0.310相应的锰含量为0.035%。
实践证明,“增量光度法”比“标准加入法”更简便而切合实际 [20]。
3.7. 光度法测定结果的不确定度
从本文3.3可知,遵循“精密度法则”的光度法样本测定,与JJF1059.1-2012《测量不确定度评定与表示》 [21] (以下简称“规范”)的重复性测量一致。“规范”之4.3.2.6指出,被测量的n次重复测量的平均值
的A类标准不确定度为:
(5)
统计学指出,
是测定“小样本”平均值
的实验标准差,它表明
落在
和
两个区间的概率分别为0.9545%和0.9973% [22]。“规范”之4.5指出,这两个包含区间的半宽度就分别是
的两个扩展不确定度:
(6)
(7)
S是样本观察值Xi的标准差。根据“规范”4.3.2.6之要求,“小样本”容量应取10。这时“小样本”必然近似正态分布,所以X10的S可按照极差法
评估。n = 10,则
,
。将
代入式(6)、式(7),即可得到不确定度的测量模型:
(8)
(9)
测量模型式(8)、式(9)表明,“小样本”均值
的不确定度与样本极差成正比,与样本容量的平方根成反比。实践证明,它们是“规范”要求的“在任何给定被测量的测量值实际可达到的最小测量不确定度”,比“合成法”评定结果简明而切合实际 [18] [23]。
3.8. 不确定度与允许误差的统一
实验室的日常检测结果都有允许误差要求,而当前国家对实验室测量结果又有了不确定度要求 [24],所以应当使两者统一,光度法的不确定度测量模型具备了这样的条件。因为无论不同实验室的“人员、器械、物料、方法、环境”多么不同,只要各自都遵循“精密度法则”,检测相同化学物质的“人员、器械、物料、方法、环境”检测能力必然是确定的,同一化学物质的同一个测定系列,就只能有一个的正常极差R (超常极差会在排除统计离群值中被清除),所以各自样本的不确定度就只决定于各自样本的容量。如果设定各自样本测定的允许误差为
,它就是该物质日常检测结果的“约定不确定度”。已知容量为n“小样本”的不确定度是U95和U99,则“约定不确定度”
的“小样本”容量nX就应分别为:
(10)
(11)
比如,表2碳钢中锰、硅、磷的10次测得值,锰的允许误差
,不确定度U95 = 0.008%;硅的允许误差
,不确定度U95 = 0.006%;磷的允许误差
,不确定度U95 = 0.001%。根据式(10),它们的nX都为0.4 (计算过程省略),即都是一次测得值Xi就可满足允许误差要求。它们测定结果的允许误差和不确定度就统一是
。测得结果既可以允许误差方式表达为:
,也可以不确定度方式表达为:
,kp = 2。实际表2中锰、硅、磷的10个测得值中的每一个,与它们的标准值之间的误差,都没有超出各自的允许误差
,标准值也没有超出它包含概率0.95区间的半宽度
。
比表2中的U95值大,因为在遵循“精密度法则”条件下,样本容量愈小,不确定度就愈大。
式(10)、(11)对于常规检测的指导作用,证明了光度法不确定度模型的可靠性、普适性,“合成法”的评定结果就没有这种特性。也表明了“精密度法则”使光度法样本测得值正态分布的重要,因为没有样本的正态分布,就没有光度法不确定度的测量模型。
4. 结语
实践证明,“精密度法则”是光度法的基础技术。它不仅可使各种因素对同一测定系列的干扰趋于一致,显示出了光度法的真实规律,确立了“两标准光度法”,奠定了光度法测定各种含量的理论基础,改变了传统观念;而且它是正态分布理论在光度法中的具体体现,样本测得值呈正态分布。不仅易于发现系统误差和统计离群值,保证了测定结果的可靠性,而且简化了结果的不确定度评定,满足了JJF1059.1-2012《测量不确定度评定与表示》的各项要求,极有推广应用价值。
参考文献