1. 引言
湿度对人体舒适度有着重要影响,湿度的控制显得尤为重要 [1] [2]。传统的电感电容湿度传感器对环境的要求比较高,在强电场和强磁场环境中会严重影响传感器的测量精度。因此,不适合在高电压和强电场等恶劣环境中工作 [3],用光子代替电子作为信息载体,改善在传统湿度测量仪器中存在的对环境要求高、能量损耗大、效率低下等问题。二十世纪八十年代,光子晶体的概念首先是由Yablonovich [4] 和S. John [5] 提出的。光子带隙是光子晶体一个非常重要的光学特征,它被称为“光子禁带”。光子禁带可以解释为一个频率区间,即频率在此区间的光子,它的传播会被光子禁带阻断。关于光子晶体的结构,它可以由折射率不同的材料,按照一定的空间规律进行组合,使得其内部折射率按照一定的规律进行变化。光子晶体的物理结构决定了光子在其内部的运动与电子在半导体中的运动有一定的相似性。光子在光子晶体内部传播过程中会形成带状的色散曲线。在一定条件下,带与带之间将会形成光子禁带 [6]。本文以光子晶体的折射率作为研究点,研究折射率与环境湿度的关系,从另一个角度去研究光子晶体的湿度测量机理。
2. 理论模型
光子晶体是结构按照一定规律变化,晶体内部折射率从高到低,或者从低到高周期性变化的晶体结构。在一定波长条件下,光子晶体的折射率变化幅度可以达到非常大。因此,一些结构的光子晶体可能会出现与半导体禁带相似的结构 [7]。二维光子晶体相对三维光子晶体结构相对来说更简单一些,制造难度要低的多,更有利于在相关领域的广泛应用。二维光子晶体根据内部材料结构不同可以分为正方形、三角形以及蜂窝状。正方形是这三种中结构最为简单的,也就是更易于做光子特性研究的结构。本文采用正方形晶格结构如图1所示,对光子禁带进行研究。
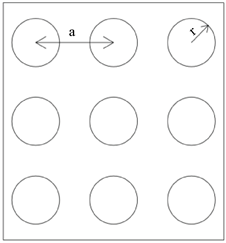
Figure 1. Schematic diagram of two-dimensional photonic crystal with square lattice
图1. 正方晶格二维光子晶体示意图
晶格周期为a = 850 nm,介质柱的半径为r = 350 nm,介质柱采用气孔率为30%的二氧化硅材料。采用折射率n1 = 1.453的SiO2、n2 = 1.329的水、n3 = 1的空气,背景介质材料SiO2的折射率和相对湿度的关系曲线如图2所示 [8]。
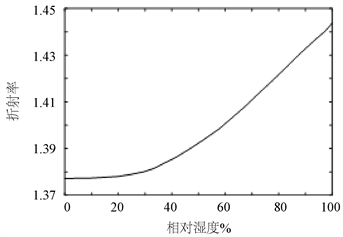
Figure 2. Relationship between refractive index and relative humidity
图2. 折射率与相对湿度关系图
图2所示的时SiO2薄膜的折射率与相对湿度关系图说明了SiO2薄膜的折射率与相对湿度的理论上的关系。通过图2可以发现折射率随着湿度的变化而变化,并且在30%~100%的相对湿度范围内精度较高。因此,可以通过测量材料的折射率来间接测量湿度值。
二维光子晶体由折射率不同的介质材料构成,介质柱选择锐钛型TiO2,选择气孔率为30%的SiO2作为背景介质。两种不同折射率的材料,按照一定的周期排列构成 [8]。随着环境湿度的变化,SiO2的折射率也会发生变化。因此,光子禁带的起始波长、终止波长和禁带宽度都会变化 [9]。本论文通过数据模拟分析不同湿度下,二维光子晶体起始波长、终止波长和禁带宽度变化的趋势,分析环境湿度和光子禁带的定量关系。
目前,国内外分析光子晶体的理论方法主要有平面波法、有限差分法、光束传播法、有限元法及传输矩阵法等 [10]。FDTD法是基于Yee网格的直接将时域Maxwell方程组转化为一组差分方程的数值算法,因其原理简单、编程方便受到广泛地应用 [11]。为了方便计算,可以对模型进行简化 [12]。通过理论模型分析光子晶体的能带结构。分析光在二维光子晶体中的分布模式 [13]。利用FDTD模型,对不同湿度下的光子晶体采用归一化的计算过程进行能带计算。归一化后各个量的关系:
(1)
c为波速,微分公式变为:
(2)
介质参数处理如下:
,
(3)
式(3)中1代表基体;2代表散射体;Ω1代表散射体;Ω2代表散体机制的分布区域,经过归一化处理后的晶格稳定性参数 [13] :
(4)
根据Bloch定理,边界外格点对应的电磁分量的值和边界里相应的格点对应的电磁分量的值,只差一个相位
,使用如下的方程进行处理 [14] :
(5)
最后通过仿真获得光子晶体的能带曲线图。
3. 数据分析
本文通过MATLAB方阵软件,仿真分析二维光子晶体的能带结构,包括禁带宽度变化、禁带起始波长变化、禁带终止波长变化与相对湿度变化的关系,来研究二维光子晶体湿度传感器的感湿机理。
根据简化后的理论模型,绘制了图3、图4正方形晶格二维光子晶体能带结构图。图3表示二维正方形晶格光子晶体在横电模式(TE)下,0%与100%湿度环境中的能带结构。光子晶体在横磁模式(TM)下,0%与100%湿度环境中的能带结构如图4所示。
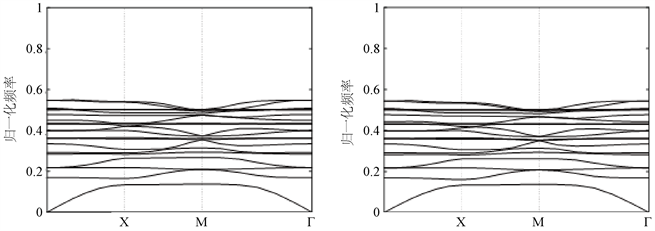 (a) 相对湿度0% (b) 相对湿度100%
(a) 相对湿度0% (b) 相对湿度100%
Figure 3. Band structure of two-dimensional photonic crystal for TE mode
图3. TE模式下二维光子晶体能带结构
图3、图4的横坐标代表二维正方形晶格光子晶体的格栅。光子的波长可以通过归一化转化公式(6)求得。
(6)
式(6)中a代表周期;w代表角频率;
代表波长。
按照上述转换关系,求出光子的波长。从能带图中可以看出,光子晶体的禁带宽度、起始波长、终止波长都发生了变化,并且在TM和TE的模式下变化不同。
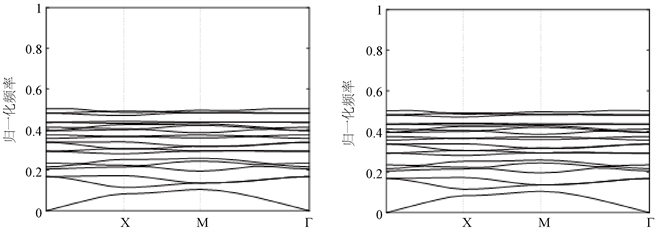 (a) 相对湿度0% (b) 相对湿度100%
(a) 相对湿度0% (b) 相对湿度100%
Figure 4. Band structure of two-dimensional photonic crystal for TM mode
图4. TM模式下二维光子晶体能带结构
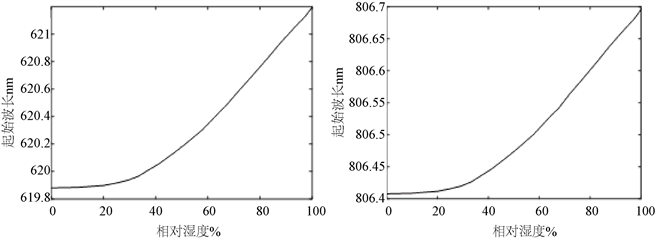
二维光子晶体的禁带起始波长在TE和TM模式下,与相对湿度的关系如图5所示。
 (a) TE模式 (b) TM模式
(a) TE模式 (b) TM模式
Figure 5. Relationship between initial wavelength and relative humidity
图5. 起始波长与湿度之间的关系
如图5所示,二维光子晶体的禁带起始波长随着相对湿度的增加而增大。在TE模式下,光子禁带的起始波长从619.881 nm增加到621.198 nm;在TM模式下,光子禁带的起始波长从806.408 nm增加到806.695 nm。湿度在30%~100%的范围内,其变化显著。从图5可以得知,光子禁带的起始波长在TM模式下比在TE模式下更大,但是在TE模式下,光子禁带起始波长的变化更大大。在40%~100%之间,相对湿度和光子禁带的起始波长趋于线性关系,经过数据拟合,其拟合公式为:
(7)
TE模式:p1 = 0.03198;p2 = 493.8。
TM模式:p1 = 0.04952;p2 = 576.8。
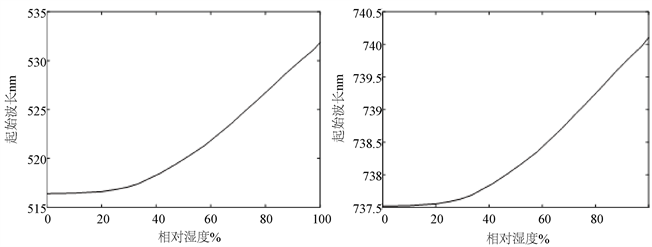
二维光子晶体的禁带终止波长在TE和TM模式下,与相对湿度的关系如图6所示。
如图6所示,正方形晶格二维光子晶体的光子禁带终止波长随着相对湿度的增加而增大。在TE模式下,光子禁带的终止波长从516.401 nm增加到531.864 nm。在TM模式下,光子禁带的终止波长从737.518 nm增加到740.106 nm。光子禁带终止波长在湿度30%~100%的范围内,变化显著。光子禁带终止波长在TM模式下比在TE模式的波长要大,但是TE模式下的波长变化大。经过数据拟合,波长与相对湿度的函数关系式为公式(7)。其中,
TE模式:p1 = 0.06678;p2 = 437.5。
TM模式:p1 = 0.008566;p2 = 631。
二维光子晶体的光子禁带禁带宽度在TE和TM模式下,与相对湿度的关系如图7所示。
 (a) TE模式 (b) TM模式
(a) TE模式 (b) TM模式
Figure 6. Relationship between termination wavelength and relative humidity
图6. 终止波长与湿度之间的关系
 (a) TE模式 (b) TM模式
(a) TE模式 (b) TM模式
Figure 7. Relationship between band width and relative humidity
图7. 禁带宽度与湿度之间的关系
如图7所示,光子晶体禁带宽度随着环境的相对湿度的增加而减小。在TE模式下,光子晶体的禁带宽度从103.479 nm减少到89.333 nm。在TM模式下,光子晶体的禁带宽度从68.889 nm减少到66.588 nm。在TE模式下的禁带宽度要比在TM模式下的大,在TE模式的禁带宽度变化范围也要更大。经过数据拟合,相对湿度与禁带宽度的函数关系为公式(7)。其中,
TE模式:p1 = −0.03481;p2 = 56.27。
TM模式:p1 = −0.04095;p2 = 54.22。
4. 结论
二维光子晶体的禁带变化与相对湿度的关系可以作为湿度传感器的感湿机理,可以实现传感器对空气相对湿度的探测。二维光子晶体在不同的湿度环境中,起始波长、终止波长、禁带宽度变化呈现明显变化。起始波长变化在TE模式下达1.317 nm,在TM模式下达0.287 nm。终止波长变化在TE模式下达15.462 nm,在TM模式下达2.588 nm。禁带宽度变化在TE模式下达14.145 nm,在TM模式下达2.301 nm。因此,在TE模式下感湿性能更好。特别是湿度在30%~100%之间,对相对湿度的探测更为灵敏。上述仿真实验结果,说明基于二维正方形晶格光子晶体折射特性的湿度传感器式理论上是可行的,可以作为未来深入研究的一个方向。
基金项目
宁波工程学院王伟明基金资助项目(2017010)。