1. 引言
随着页岩气勘探开发的深入,亟需基于微地震监测成果,综合多元数据实现复杂裂缝网络展布形态认知与评估,建立微地震震源与支撑裂缝分布的关联关系,实现页岩储层有效改造体积和产能预测 [1] - [9]。国内外在裂缝建模方面开展了大量的理论方法及新技术研究工作 [10] [11] [12],多用等效连续模型(equivalent continuum model)建立裂缝模型和流体流动模拟研究 [13]。由于受到尺度的影响,等效连续模型无法表征任意尺度上的非均质性。近两年,DFN离散裂缝网络模型(discrete fracture network model)在裂缝建模方面已得到初步应用 [2] [14]。四川威远页岩气示范区的天然裂缝十分发育,水力压裂裂缝网络复杂,常规的微地震裂缝解释与地质建模技术不能有效地反映页岩气储层水力裂缝与天然裂缝的相互作用,可靠性较差,储层改造体积分析认识对产量预测指导作用不大,无法完全满足勘探开发要求 [15]。因此,本文对威远页岩气示范区5口井开展微地震多元数据裂缝建模与产能预测工作,以提升和储备页岩气微地震监测配套技术水平,为页岩气勘探开发提供技术支撑。
2. 地质概况
四川盆地主要发育六套页岩,其中志留系龙马溪组、寒武系筇竹寺组是页岩气勘探开发最有利的层系,龙马溪组是现阶段页岩气开发的主要层系。龙马溪组整体为陆棚相沉积,沉积相带较稳定,分布范围广泛,外陆棚为页岩储层分布的有利相带 [16] [17]。威远地区页岩气储层分布在下志留统龙马溪组一段(包含上奥陶统五峰组),地层埋深主要分布在2000~3000米之间,天然裂缝较为发育。储层岩性为以黑色碳质页岩、黑色页岩、硅质页岩、黑色泥岩、黑色粉砂质泥岩为主,储层厚度一般为20~50 m,孔隙度为3.6%~6.3%,储集空间类型较多,孔隙类型包括有机孔、粒间孔、晶间孔、晶内溶孔,裂缝类型分为构造缝、成岩缝、溶蚀缝、生烃缝等 [18] [19] [20] [21]。
3. 研究方法与关键技术
3.1. 研究方法
本文在地质模型的基础上,结合水力压裂裂缝的形成过程,根据四川威远页岩气示范区的微地震资料解释压裂裂缝与水力压裂改造模型,再刻画水力压裂改造完成后形成的裂缝形态(长度、角度、裂缝密度等),采用分级裂缝建模方法建立不同区块水力压裂改造的裂缝模型。并进一步结合开发生产等动态认识,将考虑天然裂缝的地质模型与建立的DFN裂缝模型进行耦合等效模拟水力压裂裂缝的参数场,从而建立双重介质模型,最后再将耦合的双重介质模型进行数值模拟,将建模结果应用于压后产能预测。具体技术路线图见图1:

Figure 1. Technology route of crack interpretation and crack modeling
图1. 裂缝解释与裂缝建模技术路线
3.2. 关键技术
3.2.1. 裂缝解释与建模技术
微地震资料解释主要利用已有的微地震资料开展解释工作,根据水力压裂破裂机理、事件点的破裂时间先后顺序、空间组合特征和事件的可信度进行事件优选,对压裂裂缝的几何特征(缝长、缝宽、缝高),SRV体积进行解释 [22] [23] [24] [25]。
裂缝模型要真实反应水力压裂的效果,本文采用DFN裂缝建模技术建立页岩气藏压后DFN离散裂缝网络模型。DFN离散裂缝网络模型是在地质模型的基础上,结合水力压裂裂缝的形成过程,以微地震资料解释压裂裂缝与水力压裂改造模型结果等认识为指导,刻画水力压裂改造完成后形成的裂缝形态(长度、角度、裂缝密度等),采用分级裂缝建模方法建立不同区块水力压裂改造的裂缝模型 [26] [27] [28] [29]。并进一步结合开发生产等动态认识,将考虑天然裂缝的地质模型与建立的DFN裂缝模型进行耦合等效模拟水力压裂裂缝的参数场,从而建立双重介质模型,为压裂后渗流场特征分析提供依据。
3.2.2. 产能预测技术
页岩气开发主要依靠水平井分段水力压裂获得产量,页岩气井的产能与地质特征、压裂参数等密切相关。本文采用生产数据历史拟合方法,将耦合的双重介质模型进行数值模拟,确定模型的等效性和实用性。当拟合率较高时,说明建立的模型比较符合实际情况,可用于压后产能预测研究。
4. 结果
4.1. 裂缝建模及参数场等效
4.1.1. 压裂裂缝识别
微地震处理结果表明威远区块为主缝–次缝–主缝带–随机缝融合的复杂裂缝形态,以主缝为主,主缝半长在280~460 m之间,局部为次缝、天然裂缝沟通的复杂裂缝形态。采用主缝、次缝交互识别明确了主缝受最大水平主应力控制明显,次缝与区域天然裂缝或微缝相关性较好。此外,根据主缝形态、微地震事件点分布范围和点密度值域范围,通过密度体约束模拟揭示了裂缝模拟效果与微地震密度体裂缝分布范围、裂缝几何特征表现一致,为建立压裂裂缝的DFN模型提供可靠依据。
4.1.2. 压裂裂缝建模
采用分级裂缝建模方法,建立X1井区块水力压裂裂缝的DFN模型 [26]。应用确定性建模方法建立主缝和次缝的DFN模型,该类裂缝切穿目的层,主缝开度为3 mm,传导率为2000 mD∙m,次缝开度为2 mm,传导率为1000 mD∙m;应用随机建模方法建立主缝带伴生的微裂缝的DFN模型,裂缝空间分布受控于主缝带裂缝密度,裂缝长度Log-normal分布显示中值为50 m,偏差为20 m,裂缝开度为1 mm,裂缝传导率Log-normal分布显示中值为200 mD∙m,偏差为100 mD∙m;应用随机建模方法建立次缝带伴生的微裂缝的DFN模型,裂缝空间分布受控于主压裂体积外围密度,裂缝长度Log-normal分布显示中值为30 m,偏差为20 m,裂缝开度为1 mm,裂缝传导率中值为50 mD∙m。将以上所有裂缝耦合在一起,综合形成压裂裂缝的DFN离散裂缝网络模型(图2),并建立X1井区块整体裂缝的DFN离散裂缝网络模型(图3)。采用吻合度计算公式,吻合度 =
,计算X1井区块压裂裂缝模型与压裂改造模型裂缝参数的吻合度,结果显示吻合度平均为87% (表1),吻合度较高。
4.1.3. 裂缝参数场等效
等效模拟是将裂缝模型等效到地质模型的过程,也是实现裂缝模型与地质模型耦合的过程。等效模拟方法分为解析等效和数值等效两大类。由于研究区为复杂缝网,等效模拟采用解析等效的方法,即ODA等效模拟算法,计算裂缝孔隙度、渗透率、裂缝密度系数等裂缝参数场,从而建立双重介质模型。
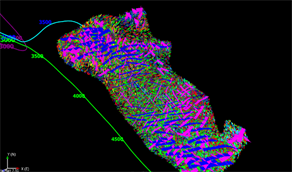
Figure 2. Diffuse Fracture Network model of fracturing cracks
图2. 压裂裂缝的DFN离散裂缝网络模型

Figure 3. Diffuse Fracture Network model of global cracks in X1 block
图3. X1井区块整体裂缝的DFN离散裂缝网络模型

Table 1. Parameter analysis table of hydraulic fracturing crack model in X1 block
表1. X1井区块水力压裂裂缝模型参数分析表
4.1.4. 试井资料动态校准裂缝参数场
试井解释技术充分利用单井实测压力数据、实际生产数据等资料进行单井基质和裂缝有效渗流能力的分析,是对裂缝有效渗流能力的重要评估技术手段。利用威远区块的地质模型、裂缝模型与实际生产数据,采用均质气藏模型,对水平井分段压裂裂缝模型进行试井解释。试井解释压力双对数曲线和半对数曲线显示,压裂效果主要体现在压裂造缝与使地层渗透率增大两方面。5口井的试井解释成果显示,除了试井数据质量较差的X1H1-2井外,其他4口井在压力双对数曲线中段均呈平行上升,呈现出压裂裂缝特征,X1H4-1井裂缝特征最明显,裂缝导流能力为525 mD∙m,表现为无限导流,X1H2-4、X1H3-5井裂缝导流能力分别为3.66 mD∙m、2.32 mD∙m,比较接近真实裂缝的渗透率(表2),同时将X1H4-1井裂缝有效导流能力3.66 mD∙m作为本区水力压裂裂缝密度优化的模拟指标。

Table 2. Well test analysis table of fracture permeability in X1 block
表2. X1井区块裂缝渗透率试井分析表
4.1.5. 裂缝渗透率分析
根据X1井区块试井测试结果,对压裂裂缝模型参数场进行校正。结果显示X1H1-2井水力压裂改造裂缝渗透率场分布Ky ≈ Kz > Kx,裂缝渗透率平均值:Kx为554.6 mD,Ky为740.6 mD,Kz为786 mD;X1H2-4井裂缝特征比较一致,水力压裂改造裂缝渗透率场Kz > Kx ≈ Ky,裂缝渗透率平均值:Kx为780 mD,Ky为740.6 mD,Kz为886 mD;X1H3-5井水力压裂改造裂缝渗透率场Ky ≈ Kz > Kx,裂缝渗透率平均值:Kx为654.2 mD,Ky为980.4 mD,Kz为1086 mD (图4为例)。表明X1H4-1井水力压裂改造裂缝渗透率效果最好,为1086 mD,基质渗透率为0.00253 mD,X1H2-4水力压裂改造裂缝渗透率效果次之,为886 mD,基质渗透率为0.00249 mD,X1H1-2井裂缝渗透率改造效果相对较差,为786 mD,基质渗透率0.0462 mD。

Figure 4. The equivalent permeability field of fracturing cracks in X1H4-1 (Kx, Ky, Kz in turn)
图4. X1H4-1井压裂裂缝等效渗透率场(依次为Kx、Ky、Kz)
4.2. 产能预测研究
本次模拟采用生产数据历史拟合方法,将建立的5个双重介质模型进行数值模拟,并进一步开展数模产能预测研究。首先对缝网压裂数值模拟模型采取人工定义SRV方法等效部分缝网压裂效果和在投产初期模拟注入相应的压裂液体积量来模拟压裂液返排的处理方式,以更好地模拟缝网压裂的效果 [30]。
4.2.1. 生产数据历史拟合
将耦合的双重介质模型采用定岩石体积方式对实际生产数据进行历史拟合,拟合结果显示日产气量和含水率与实际基本一致,拟合率较高,平均为95.4% (表3),说明该模型能够较好地体现实际的生产效果,反应压裂后气藏的渗流规律,可用于压后产能预测研究。

Table 3. Statistics table of historical fitting rate of X1 block
表3. X1井区块历史拟合率统计表
4.2.2. 压后产能预测
上文表明所建立的模型比较符合实际生产情况,为此以各井压裂前阶段末期产量为基准,采用目前的生产控制模式,使用该模型预测了各井在压裂后6年的生产动态(表4)。产量预测结果显示,生产产量与预测结果较吻合(图5为例),说明该模型具有一定的实用性,能够为页岩气的勘探开发提供指导。

Table 4. Statistics table of 6-year cumulative production of some wells in X1 block (unit: 104 m3)
表4. X1井区块部分井预测6年累积产量统计表(单位:104 m3)
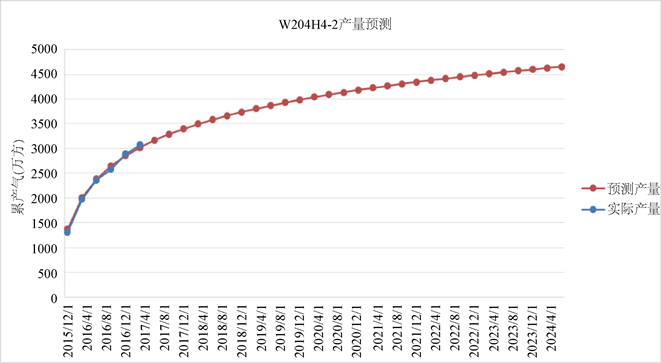
Figure 5. Cumulative production map of 6-year projection of X1H1-2
图5. X1H1-2井6年预测累积产量图
5. 结论
1) 威远区块为主缝–次缝–主缝带–随机缝融合的复杂裂缝形态,以主缝为主,主缝半长在280 m~460 m之间,局部为次缝、天然裂缝沟通的复杂裂缝形态。采用主缝、次缝交互识别,明确了主缝受最大水平主应力控制明显,次缝与区域天然裂缝或微裂缝相关性较好。
2) 不同储层类别,水力压裂改造裂缝渗透率场存在差异。X1H4-1井水力压裂改造裂缝渗透率效果最好,裂缝渗透率场Ky ≈ Kz > Kx,裂缝渗透率平均值为1086 mD,基质渗透率为0.00253 mD;X1H5平台水力压裂改造裂缝渗透率效果次之,裂缝渗透率场Kz > Kx ≈ Ky,裂缝渗透率平均值为886 mD,基质渗透率为0.00249 mD;X1H1-2井裂缝渗透率改造效果相对较差,裂缝渗透率场分布Ky ≈ Kz > Kx,裂缝渗透率平均值为786 mD,基质渗透率为0.0462 mD。
3) 采用生产数据历史拟合方法,将耦合的双重介质模型进行数值模拟,结果显示日产气量和含水率与实际基本一致,拟合率高达95.4%,表明建立的模型比较符合实际生产情况,可用于压后产能预测研究。为此使用该模型预测了各井在压裂后6年的生产动态,结果表明生产产量与预测结果较吻合,说明该模型具有一定的实用性,能够为页岩气的勘探开发提供指导。