1. 引言
近二十年来的研究认为,工作记忆中存在一个注意焦点(focus of attention),注意焦点是信息存取和加工的核心机制,其容量有限,每次只能指向一个项目,并对这一项目进行加工(Garavan, 1998; Oberauer, 2002)。而复杂认知任务通常需要对多个项目加工,在这些任务中,注意焦点就需要在项目之间转换。例如,当对一个两位数进行心算时,注意焦点首先要对个位数运算,然后要对十位数运算,在这一过程中,注意焦点需要从个位数转换到十位数。
注意焦点转换过程是工作记忆的核心认知过程之一。近年来备受关注的同中心模型(the concentric model)认为,工作记忆分为长时记忆激活部分(activated part of long-term memory)、直接存取区(region of direct access)和注意焦点三个功能区域(Campoy, 2017; Nee & Jonides, 2013; Oberauer, 2002, 2009, 2013; Oberauer & Hein, 2012; Oberauer & Lin, 2017; Oberauer, Souza, Druey, & Gade, 2013)。其中,长时记忆激活部分的项目处于被动保持的状态,这些项目可被保持较短的时间;直接存取区的项目被主动保持在工作记忆中,这一区域可保持四个左右的项目;在直接存取区中,注意焦点每次选择一个项目进行加工,这一项目为认知任务当前指向的对象,具有最高的可存取性。在这一模型中,注意焦点需要在直接存取区的项目之间进行转换,这种转换过程是工作记忆基本的执行功能之一(Verhaeghen et al., 2007)。
Garavan (1998)最早采用记忆更新任务(memory updating task)考察了注意焦点转换现象,这一任务也成为注意焦点转换研究的经典范式。在该研究中,Garavan要求被试为两种图形分别保持一个数字(项目),接下来,每次随机呈现其中一种图形,要求被试提取这一图形的原有数字,对数字进行“+1”的运算,并将运算结果作为这一图形的新的数字(对图形的数字更新)。在一个运算序列中,两种图形的数字会被多次进行这种更新运算。结果发现,当注意焦点对一种图形的数字进行运算后,如果下一次仍然对这一图形的数字进行运算(项目重复类型),则反应时较短;而如果下一次对另一种图形的数字进行运算(项目转换类型),则反应时较长。Garavan将这一反应时的差异(转换代价)解释为注意焦点从一个项目转换到另一个项目所需的时间代价。
自Garavan以来,研究者对注意焦点转换现象进行了大量的探讨(e.g., Berti, 2016; Chen, Feng, Wang, Su, & Zhang, 2016; Ecker, Lewandowsky, & Oberauer, 2014a; Frenken & Berti, 2018; Janczyk, 2017; Lendinez, Pelegrina, & Lechuga, 2015; Price, Colflesh, Cerella, & Verhaeghen, 2014; Stewart, Hunter, & Rhodes, 2019),这一现象已成为工作记忆领域研究的热点之一(Oberauer & Hein, 2012; Oberauer et al., 2018)。但这些研究主要将这一现象作为整体的过程进行考察,而对于这一现象所涉及的具体认知过程关注较少。近年来一系列的研究发现,注意焦点转换涉及复杂的认知过程,至少与四种认知过程有关,即背景存取、提取、更新和反向抑制,考察这些认知过程对于理解注意焦点转换的内在机制具有重要的意义。接下来,本文重点介绍这四种认知过程的相关研究,并指出现有研究存在的问题;然后提出一种注意焦点转换的认知过程模型,并在这一模型的基础上展望了未来的研究方向。
2. 注意焦点转换中的背景存取和提取过程
在项目转换类型中,当注意焦点需要指向一个新的项目时,这一过程又可能包括两种具体的认知过程,即注意焦点首先需要指向这一项目的背景位置(背景存取过程),然后需要提取这一项目(提取过程)。例如,工作记忆以顺序“A-B”保持两个数字,当需要对项目B进行运算时,注意焦点首先需要指向第二个系列位置,然后需要提取这一位置的项目B,在此基础上才能进行运算。
2.1. 背景存取过程的相关研究
早期研究认为,工作记忆中的项目为注意焦点指向的对象(Garavan, 1998; Oberauer, 2002)。但近年研究认为:工作记忆中的项目与特定的背景位置(如空间位置、系列位置)相捆绑,注意焦点既需要保持一个项目,也同时需要保持项目的背景位置;此外,多个项目通过其背景位置相区分,当需要对一个项目进行运算时,注意焦点首先要指向这一项目的背景位置(Campoy, 2017; Nee & Jonides, 2013; Oberauer, 2009, 2013; Oberauer & Hein, 2012; Oberauer & Lin, 2017; Oberauer et al., 2013)。根据这一观点,在项目重复类型中,注意焦点连续两次指向同一个背景位置;而在项目转换类型中,注意焦点需要指向新的背景位置(Linares & Pelegrina, 2018),因此,这种背景存取过程也可能影响转换代价。
近期,有研究直接检验了这一背景存取过程(郑允佳,胡耿丹,2020)。该研究要求被试对三种颜色的数字进行运算,在每次运算时,被试需使用一个算式(如“3 + 2”)的结果替代其中一种颜色的原有数字。在这一任务中,被试只需将算式的结果作为相应颜色的新的数字,而无需提取这一颜色的原有数字。重要的是,该研究设置一种“非更新条件”,在这一条件下,算式的结果与相应颜色的原有数字相同,运算完成后,颜色的数字不会被更新。通过这种设置,在“非更新条件”下,注意焦点既无需提取相应颜色的原有数字,也无需对这一颜色的数字更新,对于项目转换类型,注意焦点只需在三个数字的背景位置之间转换,因此,如果存在转换代价,那么其只能是由背景存取过程引起的。结果在“非更新条件”下仍然发现了转换代价,说明注意焦点转换中存在背景存取过程。
综合上述研究,背景存取过程是注意焦点转换的第一步,但现有研究主要从理论角度假设了这一过程,而对这一过程的实证研究极少。这一现状制约了研究者对背景存取过程的理解。
2.2. 提取过程的相关研究
当注意焦点指向一个新的背景位置后,还需要提取这一位置的项目,然后才能对项目进行运算,但研究者对提取过程的研究结果并不一致。一系列研究认为,提取过程是一种自动化的过程,不会影响转换代价。Bialkova和Oberauer (2010)要求被试对三种颜色的数字进行运算,并在一个运算序列中设置两种运算条件:一种为“提取条件”,这一条件要求被试每次提取其中一种颜色的原有数字,对数字进行运算(如“+4”),并将运算结果作为这一颜色的新的数字;另一种为“非提取条件”,这一条件要求被试每次将一个算式(如“1 + 4”)的结果作为其中一种颜色的新的数字,而无需提取这一颜色的原有数字。结果显示,当注意焦点转换到一个新的项目时,对这一项目的运算条件不影响转换代价,未发现提取过程对转换代价的影响。
Frenken和Berti (2018)要求被试为四个空间位置分别保持一个数字,然后每次会呈现一个线索,在线索消失后,其中一个空间位置会呈现一个运算符号(“+”或“−”),要求被试对这一位置的数字进行“+1”或“−1”的运算。该研究设置两种线索条件:一种为有效线索条件,在这一条件下,线索呈现在其中一个空间位置,接下来的运算符号也呈现在相同的空间位置;另一种为中性线索条件,在这一条件下,线索同时呈现在四个空间位置,接下来的运算符号呈现在其中一个空间位置。该研究假设,对于项目转换类型,注意焦点需要对新的空间位置的数字进行运算:在有效线索条件下,当线索呈现时,注意焦点可以预先提取这一空间位置的数字,并在运算符号呈现时直接对数字进行运算,因而反应时较短,转换代价较小;而在中性线索条件下,注意焦点无法预先提取相应空间位置的数字,因此,当运算符号呈现时,注意焦点既需要提取相应的数字,也需要对数字进行运算,反应时较长,转换代价较大。但结果显示,两种线索条件下的转换代价差异不显著,也未发现提取过程对转换代价的影响。
Campoy (2017)要求被试依次为五个空间位置(屏幕左侧、左上侧、上侧、右上侧、右侧)各保持一张初始图片,并根据记忆顺序将五张图片(及其空间位置)归为长时记忆激活部分、直接存取区和注意焦点三个区域。接下来,屏幕会呈现一个线索,在线索消失后,线索的位置会呈现一张探测图片,要求被试判断探测图片是否与五张初始图片中的一张相同。该研究将线索呈现的位置设置为两种条件:一种为初始位置条件,即线索可能呈现在五个空间位置中的一个位置,在这一条件下,探测图片可能与所在位置的初始图片相同(正性探测),也可能与五张初始图片均不相同(负性探测)。另一种为中间位置条件,即线索呈现在屏幕的中间位置,在这一条件下,探测图片可能与其中一张初始图片相同(正性探测),也可能与五张初始图片均不相同(负性探测)。结果发现,被试对初始位置条件下正性探测的反应时快于对中间位置条件下正性探测的反应时,且在初始位置条件下,只有线索呈现的位置被归于直接存取区时,才存在这一效应。Campoy认为,在初始位置条件下,当线索呈现在直接存取区的空间位置时,这一空间位置会自动激活相应的初始图片,因而将这一初始图片与探测图片进行比较时的反应时较短;而在中间位置条件下,线索呈现在屏幕的中间位置,不会自动激活初始图片,因而注意焦点需在初始图片之间搜索,与探测图片进行比较时的反应时较长。这一结果提示,注意焦点对直接存取区内的项目的提取过程是一种自动化的过程。
另一系列研究认为,注意焦点转换中包括提取过程,提取过程会增加转换代价。Linares和Pelegrina (2018)在Bialkova和Oberauer (2010)的基础上,进一步考察了注意焦点转换中的提取过程。一方面,该研究将“提取条件”和“非提取条件”分别设置在不同的运算序列中。结果发现,“提取条件”运算序列的转换代价大于“非提取条件”运算序列的转换代价。另一方面,该研究还将“提取条件”和“非提取条件”设置在同一个运算序列中。结果发现,当注意焦点转换到一个新的项目时,对这一项目的运算条件会影响转换代价,“提取条件”的转换代价大于“非提取条件”的转换代价。Berti (2016)设置“提取条件”和“非提取条件”两种运算序列,也发现了一致的结果。
综合上述研究,提取过程是注意焦点转换的关键一步,但现有研究对这一过程的考察较少,且研究结果并不一致,也鲜有研究考察这一结果不一致的原因。因此,目前尚无法明确提取过程对注意焦点转换的影响。
3. 注意焦点转换中的更新过程
在记忆更新任务中,注意焦点还需要对项目进行更新,这也可能影响转换代价。Kessler和Meiran (2006)要求被试对两种图形的数字进行运算,并将每次的运算结果作为相应图形的新的数字。该研究设置两种运算条件:一种为“更新条件”,在这一条件下,被试对图形的数字进行如“+1”的更新运算,图形的数字会被更新;另一种为“非更新条件”,在这一条件下,被试对图形的数字进行“+0”或“−0”的更新运算,图形的数字不会被更新。结果发现,当注意焦点转换到一个新的项目时,对这一项目的运算条件不影响转换代价,未发现更新过程对转换代价的影响。但在这一研究中,研究者只操纵了注意焦点转换到的项目的更新状态,而未操纵注意焦点从中转移出的项目的更新状态。
Kessler和Meiran (2006)强调,在“更新条件”下,注意焦点需要将运算结果(项目的新信息)替代相应图形的原有数字(项目的原有信息)。近年研究认为,在这一更新过程中,项目的原有信息需要与所处的背景位置解除捆绑,这种解除捆绑的过程是更新的核心过程(Chang, Ecker, & Page, 2017; Ecker et al., 2014a; Ecker, Oberauer, & Lewandowsky, 2014b; Singh, Gignac, Brydges, & Ecker, 2018)。但这种解除捆绑的过程并不是一种完全解除的过程,在运算完成后,相应的捆绑痕迹仍会被暂时储存,影响接下来的运算过程(Lewis-Peacock, Kessler, & Oberauer, 2018; Oberauer & Vockenberg, 2009)。根据这些研究,当注意焦点对一个项目更新后,这一项目的原有信息与背景位置的捆绑痕迹会被暂时储存,而这有可能影响接下来注意焦点转换到另一个项目的过程。因此,注意焦点从中转移出的项目的更新状态也可能影响转换代价。
近期,有研究借鉴上述关于更新的研究观点,既操纵了注意焦点从中转移出的项目的更新状态,又操纵了注意焦点转换到的项目的更新状态,考察更新对注意焦点转换的影响(郑允佳,胡耿丹,2020)。该研究要求被试为三种颜色分别保持一个数字。其中,实验1设置两种运算序列:“提取且更新序列”要求被试每次提取其中一种颜色的原有数字,对数字进行运算,并将运算结果作为这一颜色的新的数字;“提取序列”只要求被试提取颜色的数字,并对数字进行运算,但无需将运算结果作为相应颜色的新的数字。结果发现,“提取且更新序列”的转换代价大于“提取序列”的转换代价。实验2要求被试每次使用一个算式的结果替代其中一种颜色的原有数字,作为这一颜色的新的数字,并设置两种运算条件:一种为“更新条件”,即算式的结果与相应颜色的原有数字不同,在这一条件下,颜色的数字会被更新;另一种为“非更新条件”,即算式的结果与相应颜色的原有数字相同,在这一条件下,颜色的数字不会被更新。结果发现,“更新条件”的转换代价大于“非更新条件”的转换代价。这一研究结果说明,更新过程会增加转换代价,注意焦点转换中包括更新过程。
综合上述研究,更新过程是注意焦点转换的重要影响因素。或许由于Kessler和Meiran (2006)的早期研究未发现更新对转换代价的影响,后续研究对注意焦点转换中的更新过程关注极少。尽管近期研究发现注意焦点转换中包括更新过程(郑允佳,胡耿丹,2020),但相关研究仍极少,且鲜有研究考察更新影响注意焦点转换的机制。
4. 注意焦点转换中的反向抑制过程
当注意焦点在两个项目之间转换时,注意焦点从中转移出的项目可能会被抑制,这种反向抑制(backward inhibition)是一种重要的认知过程,但研究者对这一过程的研究结果并不一致。一些研究认为,注意焦点转换中存在反向抑制过程。这些研究采用记忆更新任务,要求被试对三个字母(郑允佳,陈琳,金志成,2014)或图形(Bao, Li, Chen, & Zhang, 2006; Chen et al., 2016)的数字进行更新运算。假设三个数字分别为项目A、B、C,当注意焦点连续进行三次运算时,这些研究设置两种刺激类型:一种如“A-B-A”类型(抑制类型);另一种如“C-B-A”类型(控制类型)。这些研究假设:在“A-B-A”类型中,当注意焦点从项目A转换到B时,A会被抑制,而当注意焦点对项目B运算1次,又立即转换到A时,因为项目A刚刚被抑制过,仍处于较高的抑制状态,因而对其运算时间较长;而在“C-B-A”类型中,当注意焦点由项目B转换到A时,因为项目A并未在之前刚刚被抑制过,因而对其运算时间较短。结果支持了这一假设,说明注意焦点转换中存在反向抑制过程。
另一些研究认为,注意焦点转换中不存在反向抑制过程。Rerko和Oberauer (2013)要求被试将注意焦点连续指向三个空间位置的颜色,并将最后一种颜色与探测颜色进行比较。在这一任务中,注意焦点无需对空间位置的颜色进行更新。假设三个空间位置的颜色分别为项目A、B、C,该研究同样设置“A-B-A”类型和“C-B-A”类型,并假设:如果存在反向抑制过程,那么与“C-B-A”类型相比,在“A-B-A”类型中,当注意焦点由项目B转换到A时,因为项目A刚刚被抑制过,所以与探测颜色比较时的正确率较低,反应时也较慢。但结果并不支持这一假设,未发现反向抑制过程。其它研究采用类似的设置和假设,例如,Rerko, Souza和Oberauer (2014)设置“A-B-A”类型和“B-A”类型(在这一类型中,注意焦点连续指向两个项目,并将后一项目与探测项目进行比较);Li和Saiki (2014)设置“A-B-A”类型和“A”类型(在这一类型中,注意焦点随机指向一个项目,并将这一项目与探测项目进行比较),也未发现反向抑制过程。
考察上述研究结果差异的原因具有重要的理论价值(Grober & Janczyk, 2014)。近年研究认为,上述研究结果的差异可能与研究所使用的认知任务的差异有关,在发现反向抑制过程的研究中,认知任务需要对项目进行更新;而在未发现这一过程的研究中,认知任务无需对项目更新,这种更新过程的差异可能导致了研究结果的差异(郑允佳,吴文春,姜荣萍,2017)。为验证这一观点,该研究要求被试对三种图形的数字进行运算,并设置三种任务条件:“提取且更新任务”要求被试每次提取其中一种图形的原有数字,对数字进行运算,并将运算结果作为这一图形的新的数字,这一任务同时包括提取和更新过程;“提取任务”要求被试每次提取其中一种图形的数字,对数字进行运算,但无需将运算结果作为这一图形的新的数字,这一任务只包括提取过程;“更新任务”要求被试每次将一个算式的结果作为其中一种图形的新的数字,但无需提取这一图形的原有数字,这一任务只包括更新过程。三种任务还设置“A-B-A”类型和“C-B-A”类型,以考察反向抑制过程。结果只在“提取且更新任务”和“更新任务”中发现了反向抑制过程,而在“提取任务”中未发现这一过程。这一结果说明,更新是产生反向抑制过程的关键因素。
综合上述研究,反向抑制过程是注意焦点转换研究的新问题,考察这一过程有助于理解注意焦点转换的内在机制。但这一过程并未引起研究者足够的关注,相关研究仍较少。此外,现有研究对反向抑制过程的研究结果并不一致,但仅有极少研究(郑允佳等,2017)考察了这一结果不一致的原因,研究者对反向抑制过程的产生机制理解较少。
5. 注意焦点转换中的认知过程:总结与展望
综上所述,注意焦点转换涉及复杂的认知过程。在现有研究基础上,本文提出一种系统的注意焦点转换的认知过程模型。如图1所示,项目A和项目B分别与背景位置1和背景位置2相捆绑,每个项目及其背景位置会同时被保持在注意焦点。当注意焦点需要从项目A (及其背景位置1)转换到项目B (及其背景位置2)时,这一转换过程可能包括四种具体的认知过程:1) 背景存取过程,即注意焦点首先需要指向背景位置2;2) 提取过程,即注意焦点可能需要提取背景位置2的项目B;3) 更新过程,即对项目A和项目B的更新也会影响这一转换过程;4) 反向抑制过程,即在这一转换过程中,项目A可能会被抑制。
这一模型可有效解释注意焦点转换中的具体认知过程。例如,在Garavan的记忆更新任务中,工作记忆以顺序“图形1的数字–图形2的数字”保持两个数字,在这一数字列中,两个数字分别与第一个和第二个系列位置相捆绑。对于连续的两次运算,假设前一次运算指向图形1的数字,那么在运算完成
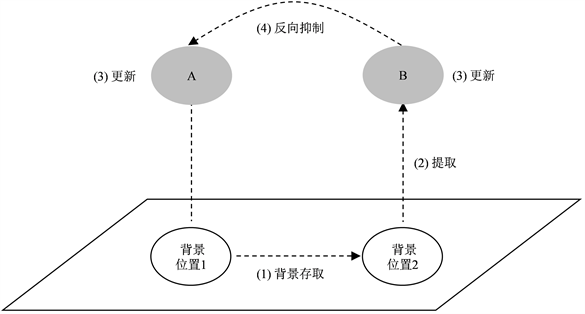
Figure 1. The cognitive processes model of switching of the focus of attention
图1. 注意焦点转换的认知过程模型
后,图形1的数字(及第一个系列位置)处于注意焦点。接下来,在项目重复类型中,注意焦点可直接对图形1的数字再次运算;而在项目转换类型中,注意焦点需转向图形2的数字进行运算。在这一转换过程中,注意焦点首先需要指向第二个系列位置(背景存取过程);然后可能需要提取这一位置的图形2的数字(提取过程);接下来,注意焦点需要对图形2的数字进行更新运算,这一更新过程(以及前一次运算中对图形1的数字的更新过程)也会影响转换过程(更新过程);最后,当注意焦点对图形2的数字运算完成后,图形1的数字可能会被抑制(反向抑制过程)。
未来可在这一模型的基础上,从三方面进一步考察注意焦点转换中的认知过程:
1) 未来研究需为四种认知过程提供更多的实验证据;同时应深入考察前人研究对提取和反向抑制过程的结果差异的原因。
2) 在四种认知过程中,背景存取和提取过程反映了注意焦点指向新项目的过程,其机制相对容易理解。但更新和反向抑制过程的机制却相对复杂,未来研究需进一步考察:更新影响注意焦点转换的机制是什么?反向抑制产生的机制有哪些?
3) 研究者采用记忆更新任务的变式,对注意焦点转换的一系列问题进行了考察,如个体差异(Bopp & Verhaeghen, 2020; Chen et al., 2016; Lendinez et al., 2015; Unsworth & Engle, 2008)、神经机制(Berti, 2008, 2016; Frenken & Berti, 2018)、记忆负载效应(郑允佳等,2014; Basak & Verhaeghen, 2011; Oberauer, 2002; Oberauer & Vockenberg, 2009)、练习效应(Oberauer & Bialkova, 2011; Price et al., 2014)、项目选择与反应选择的关系(Janczyk, 2017)等等。但在这些研究中,注意焦点转换通常包括多种认知过程,未来需进一步考察四种认知过程在这些研究问题中的作用,这也为考察注意焦点转换的内在机制提供了一个新的视角。
基金项目
本研究得到2015年度广州市哲学社会科学“十二五”规划课题(15G41)、2020年度上海市哲学社会科学规划课题(2020BSH007)和上海市浦东新区医学临床高原学科建设项目(PWYgy2018-10)资助。
NOTES
*通讯作者。