1. 引言
电力行业是国民经济发展最基础、最重要的能源产业,最近几年的电力需求增速加快、电力弹性系数剧烈波动、煤炭供给侧改革力度巨大和可再生能源稳定性不足,造成电力供需失衡。如何稳健地把握中长期电力需求发展趋势,这对电力预测的准确性提出了挑战。
众多国内外学者为提高电力预测精度做了大量研究 [1],方法大致分为两类:
1) 传统模型方法。时间序列模型(autoregressive integrated moving average model, ARIMA) [2] [3]、回归模型 [4]、灰色理论预测模型 [5]、系统动力学 [6] 等,该类模型简单、可操作性强,虽能解决中长期预测问题,但无法捕获数据中非线性和非平稳性特征,同时面对电力预测系统的复杂性,很难有较高的预测精度。
2) 智能优化算法。支持向量机回归算法 [7]、人工神经网络 [8] (artificial neural network, ANN)、自适应Boosting模型 [9]、基于遗传算法(genetic algorithm, GA)和粒子群优化(particle swarm optimization, PSO)算法的BP神经网络 [10]、基于卡尔曼滤波器和回归方法相结合的组合型算法 [11]、基于ANN与增强进化算法(IEAMCGM-R) [12] 等。这些算法都用于长期、短期的电力负荷预测。这些模型不管从精度还是处理非线性问题上,都有明显的优越性,但仍存在不足,比如计算复杂导致迭代时间过长,优化容易陷入局部最优解,还可能诱发参数敏感,导致模型出现过拟合,一定程度上影响了预测效率和精度。
因此,本文采用SBL模型分析电力需求的影响因素,筛选出关键性变量,以此来弥补传统模型在非线性和非平稳的时间序列预测偏差不足,由于不需要优化参数,将大大提高模型训练效率,同时结果更加可靠。基于KELM模型在非线性和非平稳的时间序列表现优良性能的考虑,将作为最终的预测输出模型,并引入GWO算法对KELM模型进行全局最优的参数搜索,进一步提升预测精度。引入CEEMDAN算法 [13] 做信号分解,它不仅能去除信号噪声,在处理非线性和非平稳性数据有着良好的表现,为了避免模型过拟合,将分解的各个分量,分别用于各个模型的训练,最终得到多个模型的预测结果,提升模型的泛化能力。
本文模型的优点:整体上克服非线性与非平稳性数据的不足;利用SBL模型提升了模型训练效率;利用GWO-KELM模型获取全局最优解并提升模型预测精度;利用CEEMDAN分解信号防止模型过拟合。
2. 电力需求影响因素指标体系构建
本文指标体系的构建是从宏观经济指标的角度去衡量,考虑到电力需求与经济社会发展息息相关,是经济、城市发展、人口规模、产业结构等综合因素作用的结果,结合多位学者的研究经验 [14] [15] [16],具体如下:
1) 经济发展水平。电力需求与经济发展具有高度耦合关系,经济的增长是促进电力消费增长的重要极,我们选取GDP(X1)来代表经济总量水平,人均GDP (X2)来代表人民经济生活水平。
2) 城镇化水平。城镇化也是一个预测电力需求的重要影响因素,选取城镇化率(X3)和城镇人口基数(X4)代表城镇化水平。
3) 人口总量水平。居民生活用电是电力需求的重要组成部分,选取常住人口数(X5)作为人口基数。
4) 经济产业结构。电力消耗随着国家产业结构的调整而变化,我们选取第一产业增加值(X6)、第二产业增加值(X7)、第三产业(X8)增加值来代表产业结构。
5) 工业化水平。我国电力消费主要来自于工业用电,选取工业增加值(X9)代表工业化水平。
6) 居民消费水平。居民消费与电力的需求是间接影响关系。选取消费者物价指数(consumer price index, CPI) (X10)代表居民消费水平。
7) 电力价格。考虑到价格与供需的关系,电力价格也是影响电力消费的重要因素,火力发电仍然是电力生产的主流,从而使用燃料类商品零售价格指数(X11)代替电价。
8) 用电基数。我国电力生产供应能力稳步提升,供需总体趋于平衡,通过前一期的电力数据(X12)来预测后一期的电力数据具有一定的可靠性。
3. 算法概要
3.1. 稀疏贝叶斯学习模型
本文采用稀疏贝叶斯学习模型 [17] (sparse bayesian learning, SBL),主要是考虑样本特征少于样本量时表现优秀,而且由于只需要少量参数,不仅提高模型训练效率而且结果也更加稳定,更具有可解释性。
3.2. 核极限学习机(KELM)
本文采用核极限学习机作为最终预测输出模型,它不仅能降低计算复杂度,而且使得模型更具有稳定性和鲁棒性,效率上更高,泛化性能更好。
3.3. 灰狼优化算法(GWO)
本文采用灰狼优化算法对最终预测模型进行参数优化,GWO算法是元启发式算法,具有较强的收敛性能、参数少、简单易实现等特点。
3.4. GWO-KELM模型
本文引入GWO算法对KELM进行参数优化。GWO算法具体优化KELM模型中待确定的正则化参数C和核函数gamma。为保证GWO-KELM模型在最优的条件下进行,用均方根误差(root mean square error, RMSE)作为GWO算法适应度函数,不断迭代得到KELM参数全局最优解。
4. CEEMDAN-GWO-KELM预测模型
4.1. 不同经验模态分解对比
本文选取EEMD分解、CEEMD分解、CEEMDAN分解方法进行对比。图1(a)是电力的原始分解信号,图1(b)~(d)是不同模态分解的信号,通过对比图1(e)与图1(f),可以发现CEEMDAN信号恢复具有最小的误差,这也表明它在处理非线性,非平稳信号具有良好的自适应分解能力,可以将信号按照一定顺序排列,通过提取分解后的模态函数构造滤波器实现对原始信号的降噪处理,这也是本文选取此分解法的缘由。
4.2. CEEMDAN-GWO-KELM模型
CEEMDAN [18] 分解原时间序列时,引入噪声系数来控制每次分解的噪声水平,分解成若干个IMF分量和一个残差后,通过预测各个分量加和得到最终预测值。同时GWO算法优化KELM参数,在参数取值范围内获得最优解,并且KELM模型不需要迭代,还具有出色的泛化能力。具体步骤:
1) CEEMDAN分解得到N个IMF分量。
2) GWO优化每一个IMF分量的KELM模型参数。
3) 将每次GWO得到的最优参数传入KELM模型,进行每一个分量预测。
4) 通过算术相加得到电力需求预测结果。
CEEMDAN-GWO-KELM算法的具体流程图2所示:
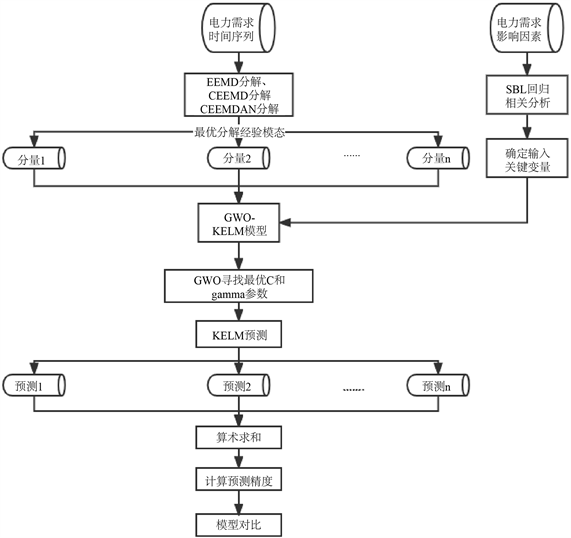
Figure 2. CEEMDAN-GWO-KELM algorithm flow chart
图2. CEEMDAN-GWO-KELM算法流程图
5. 实证分析
所选样本是我国的电力消费需求量以及12个解释变量,所有数据来源由国家统计局、世界银行、世界能源数据库。根据Alsaber Ahmad R [19] 等,使用随机森林方法填补缺失值。进行数据归一化后,将1960~2008年作为训练集,2009~2020年为测试集。
5.1. 数据平稳性检验
基于统计推断的基础下,如果数据非平稳,会破坏推断的“一致性”,基于非平稳时间序列的预测也就失去了意义。所以本文采用的方法能较好地克服非平稳数据的缺陷。
在表1中,除了X5和X11的概率P值小于0.1 (常见统计标准),即拒绝原假设,说明两个变量的数据是平稳的,其余变量均大于0.1,支持原假设,即数据是非平稳序列,数据非平稳对于常见机器学习模型可能会使得预测效果不佳。
5.2. 电力需求影响因素分析
本文选用相关性分析和SBL回归模型,综合筛选出关键性的电力需求预测指标。
如表2,我们取综合排名前5个指标,分别是:用电基数、工业增加值、GDP、城镇人口数、人均GDP。将以上的变量作为预测电力需求的输入变量,将其后的变量作为备选变量,如果加入模型后,预测效果不佳则相应剔除。

Table 2. Comprehensive variable screening ranking
表2. 综合变量筛选排名
注:变量的系数与权重值相同,排名不同的原因,是由于保留小数位数原因。
5.3. 电力需求预测模型对比
为增加模型对比说服力,控制输入相同参数值,见表3,由于其他模型,算法不同,输入参数不同,文章未列出。

Table 3. GWO-SVR & GWO-KELM model parameter explanation
表3. GWO-SVR & GWO-KELM模型参数解释
对比图3和表4预测结果:RVM和SVR预测结果最差,其次是无参数优化的KELM模型;传统ARIMA模型与GWO-SVR模型预测精度比较高,GWO-KELM与本文提出的模型具有最高预测精度。
综上说明:经过GWO优化的SVR、KELM算法预测效果都显著的优于网格搜索法;本文提出的模型,可以提升预测精度,适用于非线性和非平稳性特征的数据。

Table 4. Electric power forecast error statistics of different models
表4. 不同模型电力预测误差统计
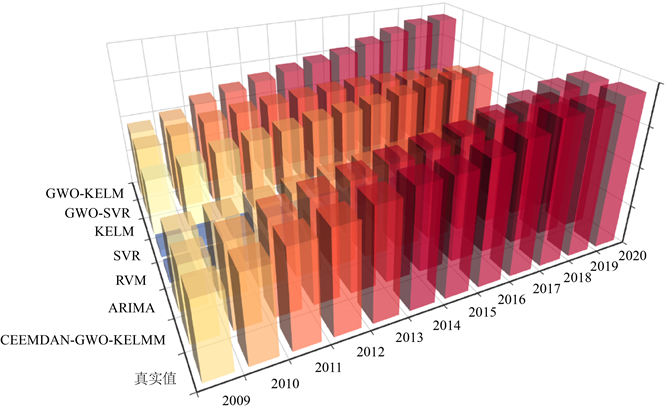
Figure 3. Comparison of power prediction results of different models
图3. 不同模型电力预测结果对比
5.4. 我国电力需求中长期预测
2021~2035年输入数据源,实际值见表5。输入变量包括:GDP、人均GDP、城镇人口数、工业增加值、用电基数。根据我国“十四五”规划的主要指标 [20],结合胡鞍钢 [21]、李平 [22] 的研究内容,实际GDP增速逐步放缓,并考虑了通货膨胀率的影响,确定了名义GDP的值,以及工业增加值。
根据孔亦舒 [23] 对未来15年人均GDP的预测,即2035年人均GDP达到中等发达国家水平目标,由于中等发达国家人均GDP水平是属于动态变化,以2020年不变价格为基础,其增长率按照4.5%计算,最终得到未来15年的人均GDP。
结合胡鞍钢等对常住人口城镇化率预测数据和杨舸 [24] 等对人口变动预测数据,计算得到城镇人口数。
根据杜忠明等对我国中长期电力需求的研判,中长期我国电力持续增长,2030年将达到11.5亿kW∙h,年均增长率为3.9%,2035年将达到13.1亿kW∙h时,年均增长率为2.6%。本文将2020年的电力需求作为2021用电基数,通过增长速率计算得到2022~2035年的用电基数。同时为了对比模型的预测效果,将无滞后一期的电力需求数据假定为未来15年电力的实际需求数据。

Table 5. Electricity demand results in China in 2021~2035
表5. 2021~2035年我国电力需求结果

Figure 4. Forecast results of different models for medium and long-term electricity demand
图4. 不同模型对中长期电力需求预测结果

Table 6. Error of medium and long-term electricity demand forecast by different models
表6. 不同模型对中长期电力需求预测误差
结合图4和表6,传统预测模型ARIMA在前期表现较好,中后期出现偏差,且逐年增大。线性回归(linear regression, LR)、贝叶斯岭回归(bayesian ridge, BR)、随机抽样一致性算法(random sample consensus, RANSAC)表现较差。贝叶斯ARD回归、泰尔森估算模型(Theil-Sen estimator, TSE)表现一般。综合以上来看,本文提出的模型预测表现最好,拥有最小的RMSE、MAE值,最大的R2。
6. 结语
从2021~2035年我国电力需求预测结果来看,“十四五”末期,我国电力需求有望达到95,709亿kW∙h,前五年平均增长率为4.96%,且增长率逐年下降。到2035年末期,电力需求将达到135,052亿kW∙h,后十年平均增长率为3.5%,增长率依然逐年下降,到2035年降至2.52%。电力需求增速放缓,但仍有上升空间,应该合理优化电力高质量发展路径,同时加强电力供需的监测预警,切实提升国民电力供应保障能力,充分满足人民对美好生活的向往,助力我国社会主义现代化强国的建设。
本文提出的方法丰富了中长期电力需求预测的研究,实验结论也为我国实现用电供需平衡、电力系统科学规划提供一定的借鉴意义。
基金项目
研究生创新项目(yjscxx2022-112-189)。