1. 引言
现阶段我国铁路运输中,旅客服务趋向高速化,货运服务趋向重载化,为铁路带来了更多的经济效益和社会效益的同时也加剧了铁路轨道状态的恶化,传统的轨道维修养护模式已经无法满足铁路运行的需求,因此就对轨道养护提出了新的要求。
目前,国内主要的轨道养护管理方法有两种模式:1) 工务部门根据综合检测列车检测发现的轨道几何尺寸超限处所,以及轨道质量指数TQI (Track Quality Index)较差的区段编制具体维修计划,即“故障修”;2) 当轨道线路累积通过的总重量超过规定的标准且轨道部件存在较多的病害问题时,安排相应的大中修或综合维修计划,即“周期修”。这两种轨道养护管理模式大幅增加了工务部门的工作量,同时对于有限的养护维修资源,如资金、养护机械等,无法做到合理安排以及科学配置,最后造成大量的资源浪费,耽误工作效率。
近些年,为了节约资源,提高效率,各行业针对工业部件老化,纷纷提出了另一种养护维修模式,即“状态修”。铁路轨道“状态修”的主要内容是基于已有的轨道几何质量状态的历史样本数据,对其进行研究总结,得到相应的轨道几何不平顺的变化规律,分析和挖掘恶化规律,在此理论基础上构建科学合理的预测模型,实现对轨道线路病害的预测和预报,具有极其重要的价值和现实意义。现阶段,随着人工智能兴起,采用机器学习的方法进行铁路故障诊断和维修决策也逐渐成为研究热点。其基本理念是针对大量的特征数据来构建分类器,分类器的效果是数据的直观反映。彭丽宇等基于BP (Back Propagation)神经网络对轨道不平顺的七个几何特征的变化规律进行预测分析,从而指导维修决策 [1]。孔德扬等则是基于BP神经网络创建了铁路安全管理模型并构建评价指标体系,为铁路维修现场的安全管理提供一定的理论基础 [2]。本文基于轨道几何特征数据构建BP神经网络模型,将铁路维修决策问题抽象为基于多维度特征的二分类问题,将是否进行铁路维修视为“0~1”变量,维修记作类别“0”,不维修记作类别“1”,定位历史维修数据构造训练集,通过挖掘不同类别下七个轨道不平顺的几何指标的数据特征,完成模型的自主学习,并输出在当前轨道特征下的维修决策。
2. BP神经网络模型
BP神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,在经过长时间的发展和迭代后,无论在理论还是在性能方面已比较成熟 [3]。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定,并且随着结构的差异其性能也有所不同。
BP神经网络的结构是一种多层前馈式神经网络,在传统网络的基础上,增加了误差向前的传播过程,如图1所示,以用于更新网络权重,逐步降低输出数据的误差。
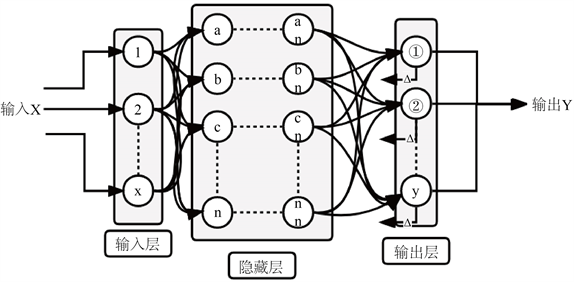
Figure 1. Structure of BP neural network
图1. BP神经网络结构
我们定义一个完整的BP神经网络模型结构:记输入层结点个数为n,隐藏层节点个数为l,输出层结点为m。
则神经网络的计算步骤如下:
1) 初始化BP神经网络。依据正态分布初始化神经网络权重矩阵w及偏置向量b。
2) 数据前向传播。输入层数据向量
经过计算,传输到隐含层:
(1)
其中
为输入层到隐藏层的权重,
为输入层到隐藏层的偏置,
为隐藏层的输出,再经过如下计算传输到输出层:
(2)
其中
为隐藏层到输出层的权重,
为隐藏层到输出层的偏置。最后,通过sigmoid函数计算输出层输出:
(3)
3) 计算模型输出误差。在二分类问题中,常采用交叉熵损失函数计算模型损失:
(4)
其中
为输入数据的真实值,即0~1变量,
为输出层的输出。
4) 误差前向传播,更新模型参数。计算公式如下:
(5)
(6)
其中
为学习率,
,
均为更新后的参数。
5) 重复步骤2)~4),通过设置最高迭代次数,或者设置两次输出误差的差值阈值来停止神经网络的更新,输出最终结果。
3. 数据处理
轨道几何不平顺的评价主要通过采用统计特征值指标的方法使轨道区段内所有测点的检测值都参与到运算中 [4],铁路工务部分普遍采用的轨道质量指数 [5] (TQI)作为一项统计特征值可以在一定程度上反映轨道区段整体不平顺状态及轨道恶化程度。
TQI以200 m长度轨道区段作为计量单元,对单元内的轨道几何进行统计,用标准差来表示单项轨道几何不平顺状态,而TQI则为一个单元内左高低、右高低、左轨向、右轨向、轨距、水平和三角坑等七项几何不平顺标准差之和,计算公式为:
(7)
其中,
,
。
但实际上,轨道不平顺评定中的七个几何质量指标各自的变化规律不尽相同,图2反应了经过一定的异常值处理并平滑后的各指标数据的时间变化特征,可以发现对于不同指标,均值、变化趋势、波动等有着明显差异。目前国内外研究 [6] [7] 对轨道几何状态的评价要么采用轨道TQI指数,通过综合各个指标的方差特征来反映总体轨道质量特征,要么采用独立的几何指标,可能会导致对轨道状态的评价忽视掉部分数据特征,无法充分反映各个轨道指标的变化规律。
为了充分利用运检过程中收集的海量轨道数据特征,采用BP神经网络来进行建模分析,将轨道不平顺的七个几何特征指标作为输入数据,将是否维修抽象为0~1变量,0代表不维修,1代表维修作为输出,那么整个模型将被视为一个基于多维度特征历史数据的二分类问题。为了适应模型需要,本文首先对轨道不平顺的历史数据进行数据处理。
3.1. 维修点定位
本文获取国内某高速铁路轨道的几何不平顺检测数据,对原始数据进行降噪、插值、平滑等基本处理。由于缺少历史维修数据,需要完成对历史数据中维修点的定位,以构造BP神经网络模型的训练集。本文通过两步来精确寻找历史数据中的维修点。

Figure 2. Variation characteristics of different track index
图2. 不同指标的数据变化特征
若某个区段的轨道在近年来已被检修过,那么该区段的左高低标准差数据会有明显的“断崖式下跌”子序列。这类子序列是所有已检修区段都具有的代表性特征,如图3所示。
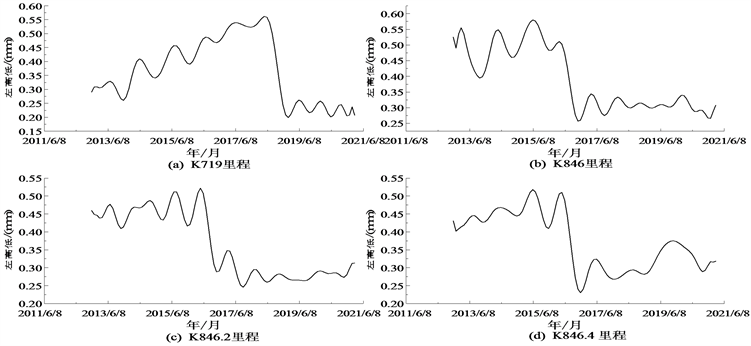
Figure 3. Track data of partial subseries
图3. 部分子序列轨道数据
使用无监督的聚类分析来区分这两类区段难度较大,因为检修带来的特征并不是全局的,而是一种局部的特征。因此可以考虑使用半监督的分类方法Shapelet方法来区分检修区段和未检修区段。
Shapelet方法是一种半监督学习分类方法,该方法的分类依据为训练集中具有代表性特征的子序列(以下简称特征子序列)。若待分类的数据集中具有一段和已知特征子序列匹配的子序列,那么就认为该数据集和相匹配的特征子序列属于同一类数据,从而达到分类的效果,如表1所示。如果在测试集上的区分效果如下:

Table 1. Distinguishing effect of the Shapelet method
表1. Shapelet方法区分效果
在历史轨道数据中,维修决策点应为表现为数据“断崖式下跌”的前一个点,表示应该在当前轨道不平顺几何特征指标值下,应该进行维修,从中可以归纳出一个重要的数据特征:维修点左侧邻近数据的平均值要比维修点右侧邻近数据的平均值要大得多,因此考虑从这个角度筛查维修点。
筛查维修点的算法步骤为:
1) 考虑数据集
,n一般较大。
2) 计算第j个数据点左侧k个数据点的均值和右侧k个数据点均值的差
,也即
(8)
3) 记使得
最大的下标为M
(9)
4) 在以
为中心的
个数据点中选取使得
(10)
(11)
5) 考虑假设检验问题
是异常点
不是异常点
否定域为:
注:算法中的
均为人工设定的阈值。
筛查算法在400个样本集中的正确率为100%,能够有效地寻找到实际进行维修的时间。
维修点定位算法部分结果如图4所示,蓝色为维修点。
3.2. 训练集构造
算法定位范围在某高速高铁上行段K3~K847共4220个里程区段,共定位到维修点1593个,令维修点所在的轨道不平顺几何特征数据的target = 1,其余数据target记为0,与原始数据中的七维轨道几何特征数据相结合,从而得到神经网络模型的训练集,部分数据如下表2所示。
4. BP神经网络模型实现及效果
将BP神经网络模型应用到铁路维修决策问题中,其网络结构的具体含义如下:
输入层:
七个轨道特征。
隐含层:经过调参选择最合适的隐含层结点数量及隐含层层数。
输出层:
。
利用python在tensorflow框架下完成BP神经网络的搭建,其能够对定义在Tensor (张量)上的函数自动求导。在神经网络训练过程中,较大的数字或者张量在一起相乘百万次的处理,使得整个模型代价非常大,并且手动求导耗时非常久,所以TensorFlow的对函数自动求导以及分布式计算,可以节省很多时间来训练模型。
建立模型过程中涉及许多参数,下面列举建模过程中的具体参数含义:
Hidden_floors_num:隐藏层的层数。较少的隐藏层无法很好的区分是否维修,会影响模型拟合效果,较多的层数又会使网络过拟合,增加训练难度,使模型难以收敛。根据选取规则以及多次数值实验对比,选择使模型效果最好的隐藏层数3层。
every_hidden_floor_num:每层隐藏层的神经元个数。同样有相应的选取规则:
(12)
其中,
是输入层神经元个数;
是输出层神经元个数;
是训练集的样本数;
是可以自取的任意值变量,通常范围可取2~10。总而言之,隐藏层和隐藏层结点数量都需要通过不断的数值实验尝试,最终选取的隐藏层神经元个数为12个。
activation:激活函数。选取Relu函数作为输入层与隐藏层之间,隐藏层与隐藏层之间的激活函数,更加有效率的梯度下降和反向传播,避免梯度爆炸和梯度下降的问题。
选取sigmoid函数作为最后一层,即隐藏层与输出层之间的激活函数,是神经网络做二分类问题最有效的激活函数。
total_step:总的训练次数。使网络收敛的迭代次数,受网络整体大小的影响,设置总迭代次数为200,000次。
precision:精度。用于计算训练模型的准确度,设置为0.5。
loss:损失函数。二分类问题最常采用的损失函数为binary_crossentropy,即交叉熵函数。
在搭建神经网络模型过程中采用交叉熵来定义损失函数,在使用神经网络做二分类或者多分类问题时,交叉熵善于学习类间特征,并且能够有效的提高模型效果较差时的学习速率,在解决二分类问题时,模型最后需要预测的结果只有两种情况,对于每个类别预测得到的概率为p和
,此时交叉熵函数的表达式为
(13)
通过构造的训练集完成BP神经网络模型的训练后,保存模型参数,即可用于预测维修结果,模型精确度由在验证集下正确输出维修决策的比率定义,在测试集模型输出结果如表3所示,其中“1”代表应该采取维修决策,“0”代表不采取维修决策,在3000条验证集数据下准确率为83.6%。

Table 3. Comparison of partial validation set
表3. 部分验证集结果对比
神经网络模型训练过程中损失函数随模型迭代次数变化图像如图5所示,其能够较为清晰的表现模型的训练效果,在超过100次迭代后模型整体损失下降速度明显降低,并最终趋于稳定。
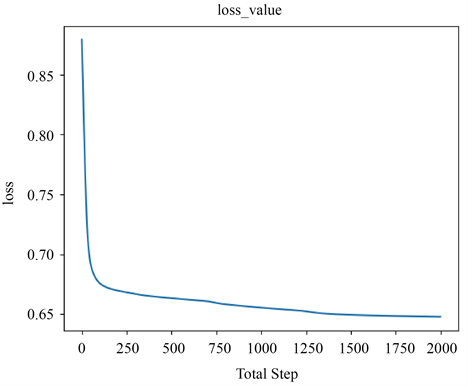
Figure 5. Changes law of loss function
图5. 损失函数变化规律
然而,在评估一个二分类神经网络的性能时,不能只看模型的准确率和损失函数,在不同类别的样本数据差距很大的情况下,模型的准确率将无法直观反应模型分类效果,因此采用AUC (Area Under Curve)值判断神经网络模型的拟合效果。AUC值同时考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。BP神经网络模型的ROC (Receiver Operating Characteristic curve)图像和AUC值如图6所示。模型AUC值为0.878,一般AUC值在0.85~0.95之间,代表着模型效果优秀。
5. 结论
随着互联网技术的飞速发展,机器学习已成为大规模数据处理和分析的主要方法。高速铁路轨道运检过程中会产生大量的轨道数据,以往轨道不平顺问题的维修决策方法往往对数据的利用率较低。本次实验通过将是否对轨道进行维修抽象成常见的二分类问题,构造BP神经网络模型,综合考虑轨道不平顺七个几何指标的数据特征,较为准确、全面地反映了轨道几何不平顺变化特征,进而进行维修结果预测,为实际的轨道维修决策提供指导。
实验根据历史轨道特征数据,准确定位了历史轨道维修点,并对应标记特征数据,构造模型训练集,提高了模型分类的准确性和科学性。但实际上,由于轨道本身存在维修不规范、不及时,以及实际维修情况受其他因素影响较大等问题,对历史维修数据的准确性产生部分影响,进而影响模型的实际效果。
总体来看,BP神经网络模型拥有较好的分类效果,且能适应复杂的样本数据。通过AUC值来看,模型的性能较高,结果具有较高的实践价值。BP神经网络模型训练时,输入轨道不平顺的七个几何指标的样本数据,经过迭代后,不断减少模型损失。完成模型训练后,保存所有训练参数,可以在后续使用时直接调用参数,输入轨道几何特征数据,输出轨道维修决策。
NOTES
*通讯作者。