1. 引言
尽管深度神经网络(Deep Neural Networks, DNN)在各种图像任务中表现优良,例如在图像分类领域 [1] ,但研究表明对待识别的样本插入微小不可见扰动形成的对抗样本可导致神经网络的给出错误分类 [2] 。在已提出的对抗样本攻击方法中,主要分为白盒攻击和黑盒攻击。在白盒条件下,攻击者具备或者有能力获取神经网络模型结构、参数等先验知识,攻击者能生成对此模型更有针对性的对抗样本 [3] ,现已提出了大量白盒攻击方法,如FGSM (Fast Gradient Sign Method) [4] 、I-FGSM (Iterative Fast Gradient Sign Method) [5] 和MI-FGSM (Momentum Iterative Fast Gradient Sign Method) [6] ,这些攻击方法需知道给定模型的梯度信息。与白盒攻击相反,黑盒攻击无法获取攻击模型的结构、参数等相关知识。
对抗样本具有迁移性,即利用一个模型生成的对抗样本能成功地攻击另一个模型 [7] ,迁移性的存在能够使得攻击者在无法获得模型结构和参数的黑盒攻击中,使用已知模型生成对抗样本来完成攻击 [8] 。现有的基于梯度的攻击方法,在白盒攻击中,有着较高的攻击成功率,但在黑盒条件下,攻击成功率却不理想,上述问题被认为是对抗样本的过拟合现象 [9] ,导致其生成的对抗样本迁移性不足。若能提升对抗样本的迁移性,将会增加对抗样本的黑盒攻击成功率。
为提升对抗样本的迁移性,本文使用图像的仿射变换和梯度细化来对样本的生成过程进行优化。主要工作如下:
1) 使用图像的仿射变换来增加对抗样本的泛化能力,从而缓解过拟合问题,提高样本迁移性。
2) 使用梯度细化方法来消除图像随机变换所带来的消极噪声梯度,降低消极噪声梯度对对抗样本泛化能力的影响。
3) 在ImageNet数据集上进行了单模型攻击和集成模型攻击实验,并与I-FGSM [10] 和MI-FGSM [11] 方法进行对比。
2. 相关工作
2.1. 对抗样本的生成方法
有研究表明,对抗样本能对深度神经网络进行攻击 [10] 。Szegedy等人 [11] 指出,深度神经网络在对抗样本的攻击下是极其脆弱的,并提出了一种基于优化的L-BFGS方法。Goodfellow等人提出了快速梯度符号法,此方法仅使用单次梯度计算来生成对抗样本,来减小生成对抗样本的计算代价。Alexey等人将此方法扩展为了迭代版本,大大增加了白盒攻击的成功率,并表明生成的对抗样本能够存在于物理世界中。Donger等人提出了一种基于动量的迭代方法,对梯度的更新方向和其收敛过程进行了优化,此方法还通过同时攻击一组网络来提高提高其迁移性 [12] 。
2.2. 对抗样本的防御方法
面对对抗样本的安全威胁,现已提出了许多方法来防御对抗样本。其中,对抗训练 [8] 是一种常用的方法,该方法提出在训练数据集中添加对抗样本来对模型进行训练,以此来提高模型的鲁棒性。Tramèr等人 [12] 提出了一种集成对抗训练的方法,来弥补对抗训练过程中的不足,即训练其他的模型,并使用其传递过来的扰动对训练数据进行增强。Guo等人 [13] [14] [15] 利用随机的图像变换,使得图像在保持关键视觉内容的同时消除对抗扰动。Prakash等人 [16] 提出一种像素偏移和软小波去噪相结合的框架,以抵御对抗样本。
3. AF-R-MI-FGSM方法
在本节中将对本文提出方法和基于梯度生成对抗样本算法AF-R-MI-FGSM (Affine And Refine Momentum Iterative Fast Gradient Sign Method)进行详细描述。定义x为输入的原始干净样本,
为样本的真实标签,
为模型参数,
为损失函数。在对抗样本的生成过程中,需要使损失函数
最大化,以此来生成一个与原始样本x在人眼上难以区分的
来欺骗深度学习模型,从而让模型给出一个错误的分类结果。对于扰动大小的限制,本文使用无穷范数来进行制约,即
。
3.1. 基于梯度生成方法
FGSM是此类方法中最早提出的,利用梯度信息来生成对抗扰动,并对扰动使用无穷范数限制,其更新公式如下,
(1)
FGSM沿着梯度的方向,仅使用单步添加扰动,来达到快速生成对抗样本的目的。但单步变化不够精准,导致其白盒成功率偏低。
I-FGSM是在FGSM的基础上增加了迭代的过程,将FGSM中的梯度进行多步迭代计算,使其梯度变化更为精准,提升了方法的白盒成功率。其公式如下,
(2)
其中,
函数是将对抗样本限制在原始样本x的
领域内,
为步长,
为迭代次数,
。
I-FGSM使用了迭代来逐步生成扰动,使其梯度变换更为平稳,但由于迭代的次数增加,生成的对抗样本会出现过拟合现象,导致其迁移性降低。
MI-FGSM是在迭代的过程中使用动量,此方法能够稳定梯度的更新方向并且能避免局部的极大值问题,其公式如下,
(3)
其中,
是动量的衰减因子,
是迭代时的累积梯度。
MI-FGSM使用动量来解决局部最优值的问题,来提高对抗样本的迁移性。
为了进一步提升对抗样本的迁移性,增加其黑盒攻击成功率,本文提出了一种基于仿射变换和梯度细化的生成方法,来缓解对抗样本的过拟合现象,提高对抗样本的迁移性。
3.2. 基于仿射变换和梯度细化生成方法
在深度神经网络训练中,数据增强是一种常用的用于解决过拟合问题的方式,本文采用一种仿射变换的数据增强方式来缓解生成对抗样本中的过拟合现象,AF-MI-FGSM方法。图像的几何变换有很多种,其中包括一些基本变换(如平移、旋转、裁剪等),图像的仿射变换就是将基本变换进行组合,来实现一种更加复杂的图形变换。本文则采用平移和旋转的组合来对原始样本进行变换。该方法在每次迭代的过程中,对原始样本以概率p进行随机的仿射变换,以此增加对抗样本的迁移性,其变换公式如下,
(4)
公式(4)使用变换函数
对原始样本进行随机的仿射变换,即对图像进行随机度数的旋转,在旋转的基础上对图像进行水平和垂直方向上的平移变换。转换概率p控制着原始样本转换的比例,以此方式来平衡生成样本的白盒和黑盒攻击成功率。
由于图像的变换的随机性,导致其生成的噪声梯度具有随机性。这种随机的噪声梯度所生成的扰动,将其加在干净的样本中,能够增加对抗样本的迁移性。然而与此同时,随机梯度中也存在部分噪声梯度,会抑制对抗样本的迁移性。为了缓解随机性带来的消极影响,同时保证对抗样本的迁移性,本文使用梯度细化方法来缓解消极梯度影响,AF-R-MI-FGSM。即相同图像经随机变换后所产生的n次噪声梯度,使用n次噪声梯度的均值来生成扰动,具体公式如下:
(5)
(6)
. (7)
公式(5)对图像
计算n次噪声梯度,由于图像输入模型采用的是随机变换处理,所以图像多次计算的噪声梯度是不同的。通过对多个噪声梯度求平均梯度,可以抵消部份的消极梯度,突出有效的梯度信息,如公式(6)所示。最后利用公式(7)来更新噪声,生成对抗样本。
3.3. 算法描述
上述的攻击方法属于FGSM家族中的一员,AF-R-MI-FGSM通过调整不同的参数设置,可以转换为FGSM家族中的其他方法,当
,即仅使用单次梯度信息进行迭代时,AF-R-MI-FGSM退化为AF-MI-FGSM。当转换的概率
时,即不对图像进行处理,仅使用原始样本生成对抗样本,方法则退化为MI-FGSM。具体转换关系如图1所示。
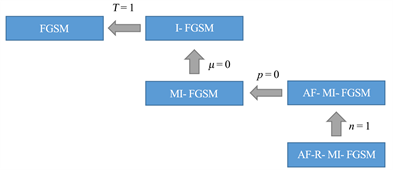
Figure 1. Conversion relationships between different methods
图1. 不同方法之间的转换关系
算法伪代码如下:
算法1:AF-R-MI-FGSM (单个模型)
输入:原始样本x以及其对应的真实标签
,神经网络f和损失函数L,扰动大小
,迭代次数T,衰减因子
,每张图像的平均梯度次数n。
输出:对抗样本
1)
2)
3) for t=0 to T do
4) 通过公式(4)
求取
5) 通过公式(5)计算模型的损失函数并得到梯度
6) 对同一张图片进行n次梯度计算,
7) 通过公式(6)对上述n次梯度求均值,得到梯度g
8) 通过公式(7)更新
9) 返回对抗样本
。
3.4. 集成模型攻击
Liu等人认为,使用集成模型能够生成迁移性更强的对抗样本。由于对抗样本对多个深度神经网络保持对抗性,那么其更能够迁移到其它的分类网络中。因此,本节使用AF-R-MI-FGSM方法攻击集成网络来进一步提高样本的迁移性。
本文遵循文献 [6] 的策略,使用AF-R-MI-FGSM方法同时攻击多个网络,将多个网络的逻辑激活融合在一起,称此为逻辑集成。具体融合方式如下:
(8)
其中
表示参数为
的第K个网络的逻辑输出值,
表示多个网络的集成权重,并满足
且
。
算法伪代码如下:
算法2:AF-R-MI-FGSM (集成模型)
输入:原始样本x以及其对应的真实标签
,K个神经网络
,其对应的网络逻辑值
和网络集成权重
,扰动大小
,迭代次数T,衰减因子
,每张图像的平均梯度次数n。
输出:对抗样本
1)
2)
3) for t=0 to T do
4) 通过公式(4)
求取
5) 将
输入到每个网络,并得到其对应的逻辑值
6) 计算集成的逻辑值
7) 根据集成逻辑值求取梯度,得到梯度
8) 对同一张图片进行n次梯度计算,
9) 通过公式(6)对上述n次梯度求均值,得到梯度g
10) 通过公式(7)更新
11) 返回对抗样本
。
4. 实验与结果分析
本节将对上述方法进行实验来验证其有效性,在单个模型和集成模型上都做了大量的实验来进行对比。在实验中,本文所提方法将与FGSM系列方法中的I-FGSM和MI-FGSM进行对比。

Table 1. The success rate (%) of single model attack
表1. 单模型攻击的成功率(%)

Table 2. The success rate (%) of integrated model attack
表2. 集成模型攻击的成功率对比(%)
4.1. 实验设置
数据集。本文使用ImageNet数据集,从其验证集中随机选取1000张图片,共选取了1000个类别,即每一个类别选取了一张图片。所选取的图片都能够被本文所使用的分类网络正确分类。所有的图片大小都预先调整为299 × 299 × 3。
网络模型。在本文中,一共选取了6个网络模型,包含四个正常训练的网络模型,Inception-v3 (Inc-v3) [17] ,Inception-v4 (Inc-v4) [18] ,Inception-Resnet-v2 (IncRes-v2) [19] 和Resnet-v2-101 (Res-101) [19] 和两个经过了对抗训练的网络模型,adv-Inception-v3 (adv-Inc-v3)和ens-adv-Inception-Resnet-v2 (IncRes-v2-ens)。
实验细节。本文超参数的选择按照文献 [6] 中的设定,迭代次数
,扰动量大小为
,步长为
。对于MI-FGSM,其衰减因子
,对于随机变换函数
,其转换概率
。对于公式(5)中对图像求
次梯度,最后取平均梯度进行计算。
评价指标。在对抗样本的攻击领域中,采取对抗样本的攻击成功率(Attack success rate, ASR)来评价攻击算法的好坏,即被攻击模型的分类错误率。但在不同的攻击算法中,ASR有着不同的含义,本文采取无目标攻击的方式,即所生成的对抗样本能够使得分类网络给出一个与真实标签不一致的结果即可,无需使其分类为指定类别。因此,本文使用的ASR可被定义为:
(9)
4.2. 单模型攻击
本节中,使用单个深度神经网络来生成对抗样本,对分类模型进行攻击。实验使用I-FGSM、AF-R-I-FGSM以及MI-FGSM、AF-R-MI-FGSM方法,分别在在四个正常训练的网络模型上生成对抗样本,并在所有的6个网络模型(包括四个正常训练的网络模型和两个经过了对抗训练的网络模型)上进行攻击。实验结果如表1所示。
表1中的结果表明,AF-R-I-FGSM和AF-R-MI-FGSM方法在黑盒设定下的攻击成功率高于其它攻击方法并且在白盒设定下也保持着较高的攻击成功率。例如,使用Inc-v3网络模型,来生成对抗样本,攻击正常训练的网络模型Inc-v4时,AF-R-MI-FGSM方法的黑盒攻击成功率达到了70.8%,而I-FGSM和MI-FGSM仅有21.8%和42.1%。攻击对抗训练的网络时也表现出了良好的性能,在IncRes-v2网络上使用MI-FGSM和AF-R-MI-FGSM方法生成的对抗样本进行黑盒攻击,其平均攻击成功率分别为33.8%和51.5%。与MI-FGSM相比,AF-R-MI-FGSM的整体平均黑盒攻击成功率提升了14.3%。说明了将仿射变换和梯度细化引入到对抗样本的生成过程中,能有效的增强样本的迁移性,从而提升其在黑盒条件下的攻击性能。
在仅使用仿射变换,即AF-MI-FGSM方法,生成的对抗样本的攻击成功率均低于使用了梯度细化的攻击方法,AF-R-MI-FGSM。如表1结果所示,AF-MI-FGSM方法的平均黑盒攻击成功率为37.2%,而AF-R-MI-FGSM方法的平均黑盒攻击成功率为46.6%,提高了9.4%。证明了使用梯度细化能够在一定程度上缓解因随机变换所产生的消极梯度影响。
4.3. 集成模型攻击
表1的结果表明AF-R-MI-FGSM方法能提高对抗样本的迁移性,但还能够使用集成网络来生成对抗样本,进一步提高其黑盒攻击成功率。实验遵循文献 [15] 的设定,通过集成多个网络的逻辑值,来生成对抗样本。本实验集成四个正常训练的网络模型,使用I-FGSM、AF-R-I-FGSM以及MI-FGSM、AF-R-MI-FGSM方法来生成对抗样本,并在所有的6个网络模型上进行攻击测试。在实验中,迭代次数
,扰动大小
,集成模型使用相等的集成权重,
。其实验结果如表2所示。
表2的结果表明,使用AF-R-MI-FGSM方法在集成模型上生成的对抗样本,其黑盒成功率更高。例如,AF-R-MI-FGSM方法生成的对抗样本攻击经过对抗训练的网络时,其平均黑盒攻击成功率为47.5%,而MI-FGSM仅有25.4%,提高了22.1%。同时,在白盒攻击方面,AF-R-MI-FGSM也保持着较高的成功率,均在90%以上。
4.4. 超参数研究
4.4.1. 转换概率p对攻击成功率的影响
本节研究不同转换概率对AF-R-MI-FGSM方法的影响,使用AF-R-MI-FGSM方法在四个正常训练的网络的集成来生成对抗样本,并在所有的6个网络上进行测试,以此来评估不同转换概率对于攻击成功率的影响。转换概率p从0以0.1步长增加到1,其他超参数设置,迭代次数
,扰动大小
,动量衰减因子
。
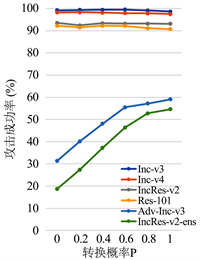
Figure 2. The influence of different conversion probabilities on the success rate of the attack
图2. 不同转换概率与攻击成功率的关系曲线图
实验结果如图2所示,其中Inc-v3、Inc-v4、IncRes-v2、Res-101表示,AF-R-MI-FGSM方法在正常训练的网络模型上的白盒攻击成功率。adv-Inc-v3和IncRes-v2-ens则表示,在使用了对抗训练的网络模型上,进行黑盒攻击,其成功率的变化趋势。实验结果表明,随着转换概率p的增大,其白盒成功率是逐步降低的,但趋势平稳且还保持着较高的成功率。其黑盒的攻击成功率随着转换概率p的增加而不断地增加。
4.4.2. 扰动大小 对攻击成功率的影响
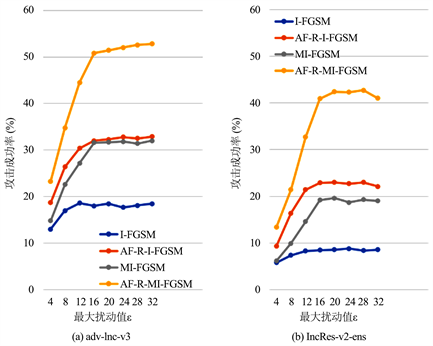
Figure 3. Graph of the relationship between different disturbance magnitude and attack success rate
图3. 不同扰动大小与攻击成功率的关系曲线图
本节研究不同扰动大小对各方法的攻击成功率的影响,实验使用I-FGSM、AF-R-I-FGSM以及MI-FGSM、AF-R-MI-FGSM四种方法,将四个正常训练网络进行权重相等的集成,以此来生成对抗样本,并分别在两个对抗训练的网络上进行黑盒测试。本实验所设置的转换概率为
,扰动大小
从4以4步长增加到32。图3中的(a) (b)分别为攻击对抗训练网络adv-Inc-v3和IncRes-v2-ens,其中实线表示其黑盒攻击成功率的变化。实验结果表明,攻击成功率开始会随着扰动的增大而增大,当到达一个峰值后成功率其成功率会趋于平稳。
5. 结束语
基于仿射变换和梯度细化的对抗样本生成方法,使用数据增强技术来缓解模型的过拟合问题,使用梯度细化来解决随机变换带来的消极梯度影响,来提高对抗样本的迁移性。此外,通过使用集成模型进一步提升了对抗样本的迁移性。与MI-FGSM方法相比,AF-R-MI-FGSM方法单模型攻击的平均黑盒攻击成功率提升了14.3%,集成模型攻击的平均黑盒攻击成功率提升了22.1%。本文还对不同的转换概率进行实验研究,给出了最优参数建议。使用了梯度细化来消除随机变换带来的影响,对于非基于梯度的攻击方法不适用,寻找一种不需要梯度信息来消除随机变换影响的方法是今后探索的方向之一。
基金项目
广州市重点领域研发项目(202007010004)。