1. 引言
随着信息网络技术的发展,人们使用网络进行社会活动的现象越来越普遍,同时使用网络的人数也在不断增加,在网络不断便利人们的同时,也产生了一系列与网络安全和信息安全相关的问题 [1] 。NAYUTA算法作为分组密码学的一种,通过根据时间进行对称加密、将随机数作为混淆依据等加密方式,使得密文达到近似理想的OTP加密 [2] 特点,为分组密码的研究提供了新的思路和方法。
2. NAYUTA算法设计
2.1. NAYUTA算法介绍
对于一次迭代而言,NAYUTA将明文消息编码为二进制序列,划分为固定大小的块(Block),令明文编码后的二进制序列为
将其划分为若干等长的块并由第一个块开始,按照顺序方式或逆序方式对块进行标号如图1所示。

Figure 1. Sort of the plaintext blocks
图1. 明文块的排序方式
对S的标号无论是顺序方式还是逆序方式,均有单密钥和双密钥两种置换方式。若使用单密钥方式,令块的固定长度为t,此时密钥空间K的大小为
;此时,若使用顺序–单密钥方式进行加密,则选取(1,
)中的任意一个数R作为密钥 [3] ,则置换后各个块的标号为
,并将S与
形成双射形式如图2所示。
若使用顺序–双密钥方式,则选取(1,
)中的任意两个数T,U作为密钥,则置换后各个块的标号为
,并使用线性探测的方法处理标号冲突,并将S与
形成双射形式;逆序–单密钥方式和逆序–双密钥方式这里不再一一陈述。在所有块的
完成标号后,将使用加密函数,对所有块和密钥的标号和数字进行变换,对于NAYUTA的软件层面加密来说,密文为有符号整数,对于NAYUTA的硬件层面来说,NAYUTA为无符号的整数(byte流)。在整体密文形成后,还需要使用波动函数对所有密文(包括加密后的密钥)进行处理,该步骤是为了增大对密文的混淆程度,增加线性密码分析攻击 [4] 和差分密码分析攻击 [5] 等密码分析攻击的难度。
2.2. 利用二叉树结构对数据进行处理
NAYUTA在进行数据处理时可以使用公式计算的方式,也可以使用二叉树结构进行数据处理,对于双密钥的情况来说,可以使用该结构实现对块(Block)的标号。
在使用二叉树结构进行数据处理时,通过建立一个t层(t为2.1节中提到的块的固定长度)满二叉树,根据顺序方式或逆序方式对每个二叉树的根节点变量a进行标号,再根据置换规则对每个二叉树的根节点变量b进行标号;根据输入的二进制流和固定长度依次对二叉树的每个节点进行判断;若为顺序方式,则二叉树节点分布规律为“左0右1”,若为逆序方式,则二叉树节点分布规律为“左1右0”如图3所示。
2.3. 基于时间的加密函数
NAYUTA在加密函数的使用方面是基于时间设计的,在NAYUTA软件层面,通过网络获取当前时间(GMT格林尼治标准时间)或通过获取本机当前时间,根据当前时间采用三种不同的非线性加密函数 [6] 对密文进行处理如图4所示,即month函数,day函数,min函数。在NAYUTA的设计过程中,应尽量避免该加密函数组与基于时间的双因子验证模式的函数组相同。
2.4. 时间偏置函数
NAYUTA时间偏置函数是为了解决在基于时间的加密函数中因为数据传输时间而产生解密函数引用不相同的问题,目前NAYUTA的精度为分钟,该问题大多存在于发送方在某时刻的59秒时发送数据而导致接收方引用的解密函数为下一分钟所对应的解密函数,从而解得一个错误的数据。因此通过使用时间偏置函数,通过设定的参数L,可以将接收方的时间偏置到发送方当前所在的分钟,通过设定偏置函数的参数,也可以确保密文的时效区间,从而提高密文的安全性,如图5所示。时间偏置函数在设定方面是对称设计。

Figure 3. Use a binary tree structure for processing
图3. 使用二叉树结构进行处理
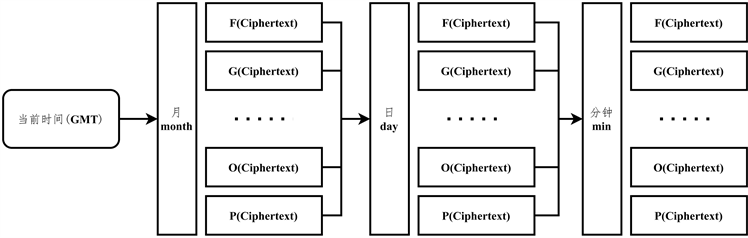
Figure 4. The processing of ciphertext by three different cryptographic functions
图4. 三种不同加密函数对密文的处理

Figure 5. The time bias function uses a schematic
图5. 时间偏置函数使用示意
2.5. 波动函数对密文(Block)的处理
NAYUTA在加密函数的过程中,除了基于时间的加密函数以外,还有波动函数需要对密文的整体进行处理,使用波动函数的目的是为了降低分组密码块(Block)重复的概率,增大NAYUTA的无序性。波动函数是一个周期函数,其周期为T,其中包含函数
;其中
为有符号整数与块(Block)相加,并得到新的块标号如图6所示。
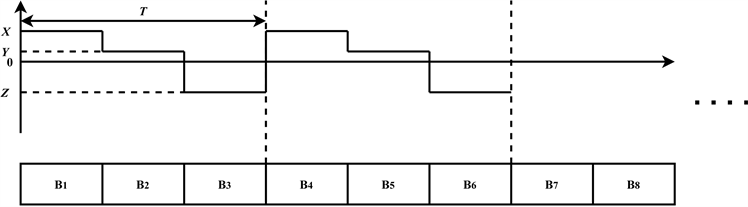
Figure 6. Schematic diagram of the processing of ciphertext (Block) by the wave function
图6. 波动函数对密文(Block)的处理示意图
2.6. 密文的组成结构与迭代
NAYUTA算法在密钥选取方式上存在单密钥,双密钥两种加密方式,对于单密钥方式,组成结构为时间戳(Time) + 密钥S + 块(Block),对于双密钥方式,组成结构为时间戳(Time) + 密钥
+ 密钥
+ 块(Block)。NAYUTA的时间戳获取的时间为本机时间,并不用作NAYUTA基于时间的双因子验证模式的依据,其组成为年–月–日–分钟如图7所示。

Figure 7. Single/double random ciphertext composition structure
图7. 单/双随机方式密文组成结构
对于NAYUTA单密钥来说,迭代一次会将除时间戳以外的所有元素(密钥与块(Block))作为明文再次进行加密,得到迭代后的密文,密文总体长度增加1个块如图8所示。

Figure 8. Single-key post-iteration ciphertext
图8. 单密钥迭代后密文
对于NAYUTA双密钥来说,迭代一次会将除时间戳以外的所有元素(密钥与块(Block))作为明文再次进行加密,得到迭代后的密文,密文总体长度增加2个块如图9所示。

Figure 9. Double-key post-iteration ciphertext
图9. 双密钥迭代后密文
3. NAYUTA算法的双因子验证模式
NAYUTA的双因子验证模式主要为密文提供了检查自身完整性的功能,主要过程为由密文因子产生验证因子,并将密文因子和验证因子混合发送。
3.1. 双因子基于时间的数据处理方式
NAYUTA双因子基于时间的数据处理方式,其所使用的时间函数规则与之前提到的NAYUTA基于时间的处理函数相同,均为通过获取本地时间或网络时间(GMT)对密文中的每个块(Block)进行处理,并产生验证因子块(Block),密文因子与验证因子集合的关系为双射关系。对于接收方对验证因子进行验证时,首先应当使用NAYUTA时间偏置函数对验证因子进行偏置,再使用其对应的时间处理函数对验证因子进行验证。在验证方式上,应当使用经过时间处理函数处理后的验证因子与密文因子进行一一对应如图10所示。
3.2. 双因子与密文(Block)的混合模式
NAYUTA在通过双因子验证模式时产生了验证因子(Block),因此在发送时采用密文因子–验证因子混合发送模式,假设排列数组为
共有n个数,将验证因子按照密文块1,X个验证因子块,密文块2,Y个验证因子块……的形式排列,当排列到N时,下一次将使用X进行排序,依次循环;当验证因子块未到N时排序完成,则将密文因子线性排列,不再插入验证因子块。验证因子块的排列方式或排列顺序与检测完整性无关,即完整性检测本身是由验证因子块所决定的。在双因子混合发送的情况下,由密文因子转换为验证因子的时间处理函数不宜为非线性函数,而应侧重线性函数,以此方式提高密文因子与验证因子混合后的无序性,如图11为双因子和密文(Block)的混合流程。该方法与干扰密钥 [7] 不同的是混合的Block能够为检测密文完整性提供判断依据。
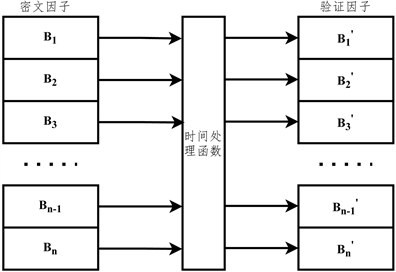
Figure 10. The correspondence between the ciphertext factor and the validation factor
图10. 密文因子和验证因子的对应关系
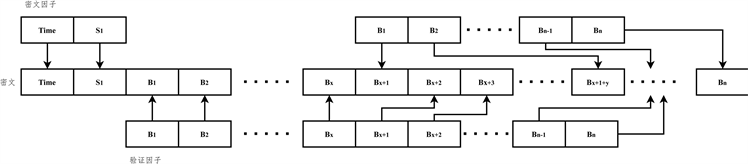
Figure 11. Two-factor and block hybrid process
图11. 双因子与密文(Block)的混合流程
4. NAYUTA算法性能测评和安全性分析
4.1. NAYUTA算法性能
将NAYUTA算法在C语言环境下加密数据,(包含双因子验证与混合模式,且块宽度为8),NAYUTA算法性能的测试机型为:
设备名称:LAPTOP-R1BOFVD4;
处理器:Intel(R) Core(TM) i5-10200H CPU @ 2.40GHz 2.40 GHz;
机带:RAM 16.0 GB (15.9 GB可用)。
在以上设备条件下,将不同数据量使用NAYUTA进行加密,得到不同数据量下NAYUTA加密的速度即表1和图12。

Table 1. The encryption speed of NAYUTA under different data volumes
表1. 不同数据量下NAYUTA的加密速度
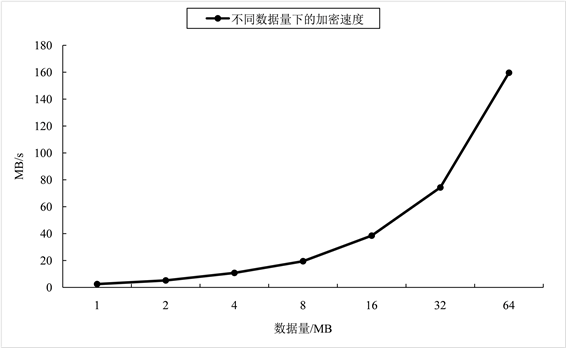
Figure 12. The encryption speed of NAYUTA under different data volumes
图12. 不同数据量下NAYUTA的加密速度
根据上图能够得到NAYUTA在数据量增大时具有较好的数据吞吐量 [8] ,能够在不同的数据量下呈现出较好的性能,取以上数据的平均值作为NAYUTA的平均加密速度,将NAYUTA的平均加密速度与其他加密算法平均加密速度相比较得到图13所示直方图。
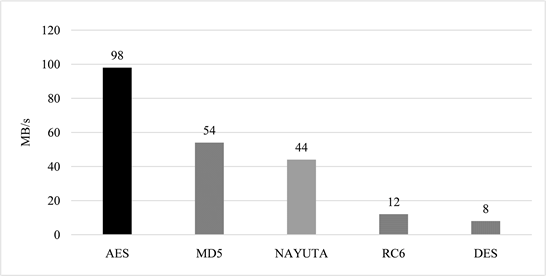
Figure 13. Comparison of the average encryption time of NAYUTA and other encryption algorithms
图13. NAYUTA和其他加密算法加密平均时间对比
能够得到NAYUTA在目前主流分组密码中的速度居中 [9] ,相较于MD5算法速度较为相近,加密速度约为AES的一半,明显快于RC6和DES [10] 加密算法。
4.2. NAYUTA算法安全性分析
对NAYUTA算法采取统计学分析的攻击方式,选取一篇文章作为明文(plaintext),该明文包含的汉字和字符共为1451个,在使用NAYUTA加密四次后(不包括双因子验证和混合模式,且分组长度为8,波动函数T = 2)产生四串密文A、B、C、D,每串密文字符平均长度为3347个,通过航天云AI [11] 相似度分析,A、B、C、D四串密文的相似度如表2所示。

Table 2. Comparison of similarities between different ciphertexts generated by the same plaintext
表2. 同一明文生成的不同密文之间的相似度对比
在不考虑NAYUTA基于时间加密的情况下,通过对比NAYUTA与ECB模式下对于同一明文的加密情况,从而对ECB在相同明文映射到相同密文下的关于明文或位图强特征的缺陷 [12] ,与NAYUTA作为不具有Feistel结构的加密算法 [13] 是如何克服这一缺陷的进行深入的安全性分析,用以证明NAYUTA在抵抗位图加密分析方面与不可能进行差分密码分析 [14] 方面的可行性。
(1)
假设具有256组无符号八位二进制强特征明文,且明文中的数据特征仅分为两种;以ECB模式将该明文的数据处理为相同格式的密文,依次排列在16 × 16的网格图中,并用F(x)分段函数对该密文的数据特征进行着色呈现如下图15。
由图15 A1可得,该密文是具有强特征缺陷 [15] 的密文,在抵抗位图加密分析和差分密码分析方面具有明显的缺陷,现在使用相同的分组长度(8位)和NAYUTA对该明文进行加密,并用F(x)分段函数对该密文的数据特征进行着色呈现如图15。得到四种位图A1、B1、B2、B3。其中,ECB位图为A1,三种密文位图依次为B1、B2、B3。三种密文采用连续加密的方式产生。由AHA方式对ECB位图与三种密文位图,三种密文位图之间进行相似度分析 [16] ,通过进行AHA的对比,能够以图形特征角度进行ECB下具有强特征缺陷的位图与经过NAYUTA算法加密后的位图相似度分析即图16。

Figure 15. Bitmap coloring image. Top left: A1; Top right: B1; Bottom left: B2; Bottom right: B3
图15. 位图着色图像。左上:A1;右上:B1;左下:B2;右下:B3
根据直方图数据,在利用AHA求得相似度后,密文数据与明文数据相似度接近四者平均值,密文与密文之间的相似度相对差异较小。
将密文数据与明文数据重新使用灰度绘制直方图并进行相关系数(Correlation) [17] 的计算,以此多角度的描述NAYUTA对具有强特征缺陷数据的扰乱作用。
(2)
由图17,根据A1、B1、B2、B3的相关系数比较能够得到,具有强特征缺陷的ECB位图与NAYUTA的三个加密位图相关系数接近三者平均值,NAYUTA的三个加密位图之间相关系数差异较大。

Figure 17. Comparative analysis of correlation coefficients
图17. 相关系数比较分析
保留相关系数比较所使用的灰度直方图,利用信息熵计算公式得到四个位图所呈现的信息熵大小 [18] [19] [20] ,如图18所示。NAYUTA算法加密下的密文约为ECB模式加密下的密文信息熵的两倍。
(3)
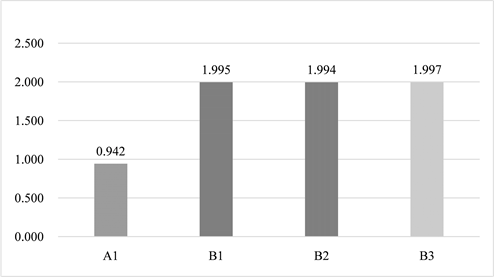
Figure 18. Comparative analysis of entropy of ciphertext information
图18. 密文信息熵比较分析
5. 结束语
NAYUTA作为基于分组密码学的加密算法,在实现方面并不完全依赖迭代来为NAYUTA提供安全性保证;在安全性实现方面,NAYUTA使用了单密钥和双密钥的方式来对所有的块进行置换操作,从而实现加密的目的,与AES、RC4等加密算法不同的是,NAYUTA并不使用密钥流与密文进行运算,相比于这两种算法,NAYUTA在加密时选取的密钥数量并不多。在分组密码的基础上,NAYUTA使用了基于时间的加密函数来对密文中的密钥和块进行加密,在检测密文自身完整性方面,NAYUTA使用了基于时间的双因子验证模式和双因子混合发送模式,通过将密文因子和验证因子混合的方式,在实现密文自身检测完整性的基础上,还解决了分组密码因加密数据量过大而导致的密钥泄露的问题。
NAYUTA将时间作为参考标准,最高精度达到1分钟,在解决时间冲突与误判方面使用了偏置函数,从而达到除去传输时间,近似于理想OTP加密模式。随机数分组作为双方对称的密钥使用,并存在于密文之中,用于抵抗线性分析和非线性分析,该模式将一般性的明文安全性与分组密码的信息熵进一步提高。波动函数用于在明文具有强特征的情况下对于分组密码的扰乱操作,能够在单位时间内抵抗线性分析和非线性分析。双因子验证模式通过将密文进行变换得到验证因子,能够抵抗重放攻击和篡改攻击。NAYUTA在一定程度上解决了密钥过长和分组密码因数据量大而安全性降低的问题。
致谢
首先,我要感谢我的指导教师,他在整个论文写作过程中给予了我很多的鼓励和帮助。在文章撰写过程中提供了许多宝贵的意见和建议。在我遇到难题和瓶颈时,给予我帮助,让我豁然开朗。
而后,我要感谢合作的老师和同学们。在这个算法中,我们共同探讨问题、设计实验、分享经验、他们的建议对论文的完成有着关键作用。
此外,我要感谢参与本研究的共同作者们。他们认真的研究精神,对我们的算法做出证明工作,使得我们的论文变得更加严谨更有说服力。
在论文写作过程中,我还得到了许多专家和同行的帮助。他们对我的研究提出了许多宝贵的意见和建议,使我受益匪浅。
最后,我要感谢我的家人和朋友。他们在我论文写作过程中给予我无尽的关爱和支持,使我能够在良好的心态下完成这篇论文。特别是我的父母,他们一直是我最坚实的后盾,无条件的支持我的想法和研究。
在此,我由衷感谢所有关心和帮助过我的人们!
基金项目
国家自然科学基金项目(62262065)、自治区重点研发任务专项项目。