1. 引言
进度作为项目管理“铁三角”目标之一,一直以来都是项目管理者关注的重点。随着经济的发展,越来越多超大型的复杂项目逐渐出现,返工也变得越来越常见,造成了项目工期的延长。因此,可以说,在新时代,进度管理仍是项目管理者眼中的一大难题,而返工作为项目进度延期的关键原因之一,也受到了越来越多的关注。
自甘特图提出以来,项目进度管理工具已经发展了好几代,目前,诸如计划评审技术等的网络计划技术仍是实际应用中的主流。然而,这些传统技术无法有效管理返工。关键链项目管理(Critical Chain Project Management, CCPM)是一种相对较新的工具,主张将各活动的安全时间提取出来统一管理,形成缓冲对抗项目执行过程中的不确定性 [1] 。然而,CCPM假设各活动是相互独立的,而在返工情境中,一个活动的工期显然受其上下游活动的影响。也即,CCPM能够管理一部分进度风险,但无法完全管理由项目返工造成的风险部分。因此,CCPM仍然不是有效管理返工的工具。由于学术界普遍认为活动间的不确定性信息流是造成返工的主要原因 [2] ,有些学者开始尝试在CCPM中引入设计结构矩阵(Design Structure Matrix, DSM)来表示活动之间的信息结构,从而考虑由返工造成的风险部分 [3] 。然而,这只是一个初步的尝试,仍有许多地方值得改进,例如,现有研究只在规划阶段初步探索了两种工具的结合,却没有考虑执行阶段的应用,且目前方法前期准备工作繁多,在实际应用中有较高的使用门槛。
总体而言,目前为止,还没有一个成熟的、能够很好管理项目返工的进度工具。因此,研究一种新的、能够有效管理返工风险的进度管理工具是非常有必要的。
2. 文献综述
2.1. 关键链项目管理
在CCPM中,缓冲是从活动中提取的安全时间的总和,它可以吸收不确定性,确保项目的按时完成。缓冲管理是CCPM的本质 [4] ,大多数关于CCPM的研究也都集中在缓冲设置和缓冲监控上 [5] 。
由Goldratt提出的剪切粘贴法(Cut and Paste Method, C&PM)是最经典的缓冲设置方法 [1] 。然而,其得出的缓冲大小会随着活动数量的增加而增加,因此可能会造成过大的缓冲区 [6] 。随后,Newbold提出了基于中心极限定理的根方差法(Root Square Error Method, RSEM) [7] 。RSEM被证明比C&PM更有效,尤其是在大型项目中 [8] 。然而,由于RSEM假定活动工期是互相独立的,而这个假设有时是不成立的,因此误差仍然存在。在此基础上,其他研究人员试图进一步考虑项目的特点和活动的信息等。例如,Tukel等人考虑了资源紧缺程度和网络复杂性 [9] ;Icmeli和Erenguc考虑了资源利用率 [10] ;Zhao等人考虑了项目经理的风险偏好 [11] 。然而,鲜有研究关注活动之间的依赖关系以及由此造成的返工风险,使得返工情形下的缓冲设置方法仍不明确。
与缓冲设置相比,在缓冲监控上的研究相对较为缺少 [5] 。本质上,缓冲监控是将缓冲消耗率与两个阈值进行比较,这两个阈值会将缓冲区分为三个部分(即绿–黄–红)。如果缓冲消耗率小于黄色阈值,则不需要对项目进行赶工;如果缓冲消耗率大于黄色阈值而小于红色阈值,则需提前计划赶工措施;如果缓冲消耗率超过了红色阈值,则需要立即采取赶工措施 [1] 。因此,缓冲监控的关键在于监控阈值的确定 [6] 。Goldratt建议将缓冲三等分(图1(a)) [1] ;Leach则认为监控阈值应该跟项目进程成比例(图1(b)) [12] ;别黎和崔南方主张动态设置监控阈值(图1(c)) [13] 。在这些研究的基础上,学者们试图更进一步。例如,Hu等人认为双阈值方法可能会降低项目绩效,因此提出了一种单阈值方法 [14] ;Zhang等人则提出了基于阶段分配的动态滚动监控方法 [15] ;此外,Hu等人还纳入了成本信息,以更具成本效益地监测项目 [16] 。然而,这些研究大多侧重项目层面的信息,而忽视了活动的特点,因此不能根据活动特征精细化管理。进一步,在存在返工的情况下,活动会因返工风险而拥有新的特征,如何在项目监控过程中有效利用这些特征值得更深入的探索。
2.2. 关键链项目管理与设计结构矩阵的结合
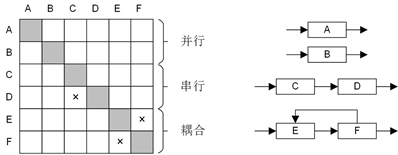
Figure 2. Information flow and activities’ logic relationships in DSM
图2. DSM中的信息流和活动逻辑关系
DSM非对角线上的单元中的标记可以表示从该单元对应的列元素到该单元对应的行元素之间的信息流(图2),因此,其在表示具有多重信息依赖的复杂系统时非常有用 [17] [18] 。进一步,DSM上三角中的标记即活动之间的逆向信息流,也即造成返工的关键信息流,从而,在研究项目返工时,其比传统的基于网络图的工具更有效 [19] [20] 。Smith和Eppinger是首批利用DSM建模项目返工的学者 [21] 。随后,Browning和Eppinger开发了第一个基于DSM的模型并开始分析返工对项目工期的影响 [22] 。从那时起,许多学者开始追随他们的脚步,利用DSM建立能描述返工过程的模型 [23] [24] [25] 。然而,正如Browning强调的,DSM只能提供项目过程的部分视图,因此不能作为独立的进度管理工具来使用 [20] 。也即,虽然DSM在返工分析中很有用,但它忽略了项目中的其他重要信息,使得项目经理无法获取足够的信息来控制项目过程。因此,DSM更像是对网络计划技术的补充,而不是替代。
许多研究表明,CCPM和DSM可以与其他技术结合。例如,CCPM与风险管理技术 [26] 和挣得值技术 [27] 结合、DSM与数据流图 [28] 和系统动力学 [29] 结合等。此外,DSM能够和基于网络图的工具一样表示活动之间的不同逻辑关系,见图2 [30] 。以上信息表明DSM具有与CCPM结合的潜力。
肖宇 [3] 首先提出了结合CCPM和DSM的想法,以期在返工情形下管理项目进度。Zhang等人 [31] 同样试图利用DSM建模活动间可能会导致返工的信息流,以更精确地计算缓冲大小。然而,他们都只讨论了一部分的返工类型,并不全面。另外,他们也没有考虑活动返工的进步曲线。随后,郝可可 [32] 在上述研究的基础上,将传统的结束–开始(FTS)逻辑关系扩展到开始–开始(STS)、开始–结束(STF)、结束–开始(FTS)和结束–结束(FTF),从而考虑活动的重叠返工,以讨论所有返工类型。然而,尽管全面讨论了返工的各种类型并考虑了进步曲线的影响,他提出的方法依托Max-plus算法,需要进行大量前期工作,应用门槛较高。最重要的是,目前的研究只集中在缓冲设置方面,忽略了缓冲监控。然而,CCPM有别于传统网络计划技术的很重要的一点就是其能在项目执行阶段为实施纠偏措施提供定量信号。因此,现有研究并不能最大程度地发挥CCPM的作用,仍需进一步优化。
综上,本文在注意到上述局限性后,尝试提出一个既能根据返工情况合理设置缓冲大小,又能依据活动返工特征精细监控缓冲消耗的缓冲管理框架,从而为返工情形下的项目进度管理提供工具。
3. 考虑返工的缓冲管理框架
本文涉及的符号及其含义见表1。
注:
、
、
均为DSM的特定表现形式;a来自Browning和Eppinger [22] 的研究。
3.1. 遗传算法优化活动顺序
如上所述,DSM上三角中的标记表示的活动之间的逆向信息流是造成返工的重要原因。然而,通过重排活动顺序,可以改变甚至简化这些信息流,从而降低项目返工风险。也即,重排DSM的行列元素,使上三角中的标记数量尽可能小,或尽可能贴近对角线,可以降低活动返工风险。
DSM元素的排序是一个NP-Hard问题,多用启发式算法解决。因此,本节采用遗传算法,以降低返工风险为目标,以迭代次数为停止准则,优化项目活动顺序。具体而言,遗传算法算子组合参考Meier等人的建议 [33] ,选择算子为锦标赛选择(Tournament Selection) [34] ;交叉算子为基于位置的交叉(Position-based Crossover) [35] ;变异算子为移位变异(Shift Mutation) [35] 。目标函数参考Zhang等人的建议 [36] :
(1)
其中,
为DSM上三角中的标记数量,
为DSM上三角中的标记离对角线的距离,455为任意指定上界,以使目标函数值始终为正。
3.2. 缓冲设置
优化活动顺序以降低项目返工风险后,即可根据活动返工信息计算项目应设置的缓冲大小。
返工类型的划分上,与前人类似,本节考虑一阶返工、二阶返工和重叠返工等三种类型 [32] ,更高阶的返工不在本文讨论范围内,因为二阶返工是高阶返工的一个基本类型,其余高阶返工与其类似。返工风险的分析上,本节引入返工概率(Rework Probability, RP)、返工影响(Rework Impact, RI)和进步曲线(Improvement Curve, IC)等三个指标 [22] 。其中,RP及RI的定义见表1,IC描述了再次执行某活动时,因为学习效应而导致的必要执行时间的减少。
如图3(a)所示,一阶返工描述了由于活动之间存在反馈信息,下游活动j在完成任务之后传递给上游活动i的信息可能与活动i最开始假设的信息不一致,因此活动i需要返工。在这种情况下,活动i的一阶返工时间计算公式如下:
(2)

Figure 3. First-order rework and second-order rework
图3. 一阶返工与二阶返工
二阶返工描述了活动j由于其下游活动k的反馈信息而需要返工,在其完成一阶返工后,由于重新执行任务而更新的信息会再次反馈(图3(b))或传递(图3(c))至活动i,造成活动i的返工。在这种情况下,活动i的二阶返工时间计算公式如下:
(3)
需要注意的是,活动k应同时为活动i和活动j的下游活动,即
且
,否则活动i和j不会因其执行信息而返工。
重叠是指本应按顺序执行的活动开始并行执行。一定程度的重叠可以缩短项目工期 [22] ,然而,也会引发不必要的返工 [37] 。如图4所示,活动i的执行需要来自活动j的信息,其本应按顺序执行,然而,由于重叠,活动i在开始执行时并不能获得由活动j输出的最终版本的信息,而只能依靠中间信息和假设开始执行。随着活动j的进行,其输出信息逐渐演变为最终版本,可能与活动i的初始输入信息存在差别,因此活动i需要返工。此时,引入
表示下游活动(图中活动i)的重叠比例,以计算其重叠返工时间 [38] 。
可通过公式(4)获得,也可由项目经理直接确定。从而,活动i的重叠返工时间计算公式如公式(5)所示。此外,需要说明的是,本文假设每个活动至多与一个前置活动重叠,与多个前置活动同时重叠的讨论可以在以往的研究中看到 [38] 。
(4)
(5)
最终,活动i的总返工时间如公式(6)所示。项目的缓冲大小可通过改进RSEM方法得到,如公式(7)所示。需要说明的是,公式(7)为项目缓冲的计算公式,接驳缓冲的计算与之类似,只需将涉及活动改为非关键链活动。为了表述的方便,本文以下部分将只描述项目缓冲。
(6)
(7)
3.3. 缓冲监控
缓冲监控可分为缓冲分配、缓冲消耗监控和赶工措施的计划与实施三个部分 [15] 。
首先,考虑返工出现的不确定性,分离出一部分缓冲吸收该部分。为此,在项目中插入一个虚拟活动,并根据项目预计返工时长占总时长的比例为其分配缓冲,如公式(8)所示。一旦活动发生返工,
即开始消耗。另外,进一步分配
是不建议的,因为返工的发生是不确定的,将缓冲分配给可能不存在的活动是一种浪费。
(8)
除返工缓冲外,其余缓冲则依据各活动的特征指标进行分配。具体来说,由于本文考虑返工风险,因此剩余缓冲将根据各活动潜在返工对项目进度的影响程度进行分配。为此,引入潜在影响关键度(Potential Effect Criticality, PEC)指标表示各活动的返工特征 [39] ,如公式(9)所示。从而,分配给各活动的缓冲可由公式(10)计算得到。
(9)
(10)
缓冲消耗监控的关键是监控阈值的确定。由于相对缓冲监控方法至今仍是从业者使用的主流方法,本节选择其作为
的监控阈值,如公式(11)~(12)所示。然而,由于返工的不确定性,其开始时间难以预测,甚至返工存在与否也不得而知。因此,无法估计项目整体返工的完成比例,也即,相对缓冲监控方法不适用。因此,
的监控阈值选用静态缓冲监控方法,如公式(13)~(14)所示。
(11)
(12)
(13)
(14)
设置完监控阈值后,即可在执行过程中追踪各缓冲的消耗率,并根据其与监控阈值的相对关系决定是否实施赶工措施。赶工措施的选择上,快速跟踪、活动崩溃、变异性降低等都是常见的做法 [40] 。本文将采用活动崩溃技术,其主张投入更多资源来减少活动的持续时间 [41] ,已在许多研究中被采用 [14] [42] 。
3.4. 缓冲管理框架
本文提出的返工情境下的缓冲管理框架总结如下:
Step 1:基于遗传算法优化活动顺序,如3.1节;
Step 2:利用分支定界法确定项目关键链 [43] ;
Step 3:利用DSM建模活动之间的依赖关系,计算活动的预期返工时间,如公式(2)~(6)。基于活动的返工情况,确定应设置的缓冲大小,如公式(7);
Step 4:根据项目的预期返工时间和活动的PEC分配缓冲区,如公式(8)~(10)。为各缓冲区设置监控阈值,如公式(11)~(14);
Step 5:执行项目;
Step 6:在各监控点处识别项目实际进度与计划进度的偏差,确定缓冲消耗率。如果缓冲消耗率小于黄色阈值,转Step 7;如果缓冲消耗率大于黄色阈值但小于红色阈值,转Step 8;否则转Step 9;
Step 7:无需赶工,转Step 10;
Step 8:计划赶工措施,转Step 10;
Step 9:立即采取赶工措施,转Step 10;
Step 10:检查项目进度,如果项目完成,则缓冲管理流程结束;否则转Step 5。
4. 算例验证
本节进行了仿真研究,以验证所提框架的有效性。算例来源于商业地产项目的可行性研究阶段 [39] ,是一个典型的具有大规模信息流的项目,曾多次应用于相似研究 [44] [45] 。在模拟中,活动持续时间被假设为来自对数正态分布的随机变量,该假设也曾应用于其他研究 [14] [31] [42] 。此外,为了简化模拟,还提出了其他假设:
l 活动至多返工一次;
l 活动的完成比例与其执行时间成正比;
l 上游活动因返工而延误时,与其重叠的下游活动会推迟开始,推迟的时间等于上游活动的返工时间 [22] 。
4.1. 算例介绍
算例项目包括19个活动和170条信息流。数据是通过与项目团队成员的访谈收集的,并根据Eppinger等人 [46] 和Hu等人 [14] 的建议进行了进一步修改。最终,活动基本信息见表2,RP矩阵、RI矩阵见图5。

Table 2. Basic information of case activities
表2. 算例活动基本信息
注:a不考虑返工风险和工期不确定性,50%完工概率的活动估计工期
。
4.2. 算例模拟过程
首先,应用遗传算法优化活动顺序。本节指定锦标赛选择算子的规模为4,获胜概率为1;基于位置的交叉算子的交叉概率为1;移位变异算子的变异概率为0.01;初始种群数为50;迭代次数为150。优化后,活动顺序转变为[C, D, H, I, G, A, E, B, F, J, O, L, P, K, Q, N, M, R, S],对应的目标函数收敛曲线如图6所示。
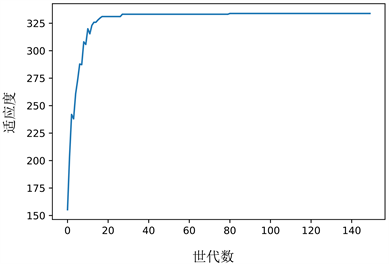
Figure 6. Convergence curve of the objective function in genetic algorithm
图6. 遗传算法目标函数收敛曲线
其次,基于优化后的活动顺序、活动之间的信息流和活动工期,利用分支定界法确定项目关键链为[C, D, H, E, B, F, J, O, L, P, K, Q, N, M, R, S]。为简化模拟,以下研究将只关注关键链活动,其重叠情况由作者随机生成,如图7所示。
然后,计算各活动的预计返工时间,分别为[0.24, 6.51, 8.74, 9.52, 0.51, 16.44, 6.05, 0.89, 2.29, 1.91, 1.08, 0.74, 0.87, 0, 0.04, 0.34]。从而,算例项目应设置的项目缓冲大小为45天。
接着,对设置的缓冲区进行分配并指定监控阈值。具体而言,考虑项目的预计返工时间,
确定为15天,监控阈值分别为0.33和0.67;各活动的PEC计算为[2.4, 6.7, 19.0, 30.6, 7.1, 30.8, 15.3, 7.8, 10.7, 10.1, 14.5, 11.7, 2.8, 3.3, 9.6, 1.7],因此,各活动分配到的
为[0.5, 1, 3, 5, 1, 5, 2.5, 1.5, 1.5, 1.5, 2.5, 2, 0.5, 0.5, 1.5, 0.5]。
的监控阈值如公式(11)~(12),其中,
,
,
。
最后,蒙特卡洛模拟项目实施过程,每0.5天监控项目实际进度与计划的偏差,确定缓冲消耗率,以决定是否采取赶工措施。赶工措施指定为活动崩溃技术,赶工后,活动持续时间的减少量可通过将原本预计用时与一个比例相乘得到,根据Vanhoucke的建议,本文将其确定为30% [47] 。
为避免随机性造成的误差,对项目实施过程进行了1000次模拟。每次模拟结束后,通过以下指标评估项目绩效:首先,项目在计划期限内完成的可能性应尽可能高。因此,考虑了实际项目工期和按时完工率两个指标。然后,项目采取赶工措施的次数应尽可能少。因此,考虑了活动赶工率(赶工活动数/活动总数)这个指标,以衡量项目过程的稳健性。
4.3. 结果讨论
首先,不使用任何缓冲监控方法,项目工期的频率和累积百分率如图8所示。本文方法计算的项目工期为113 + 45天,可以保证83%的按时完工率;不考虑返工风险的C&PM计算的项目工期为113 + 44天,按时完工率为82.2%;不考虑返工风险的RSEM计算的项目工期为113 + 24天,按时完工率为56.9%。因此,当项目面临返工风险时,本文方法计算的缓冲大小能提供更令人满意的按时完工率。此外,虽然C&PM得出的缓冲大小与本文方法相差无几,但正如2.1节所述,其比RSEM更大的缓冲是由“较高的活动数量”导致的,而非考虑活动之间依赖关系导致的返工风险。因此,其在本算例中的较好表现不可持续。而本文方法考虑了返工的深层逻辑,更为合理,得出的缓冲大小更合适。
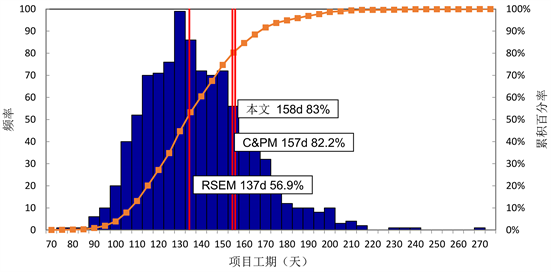
Figure 8. Comparison of buffer sizing methods
图8. 缓冲设置方法比较
然后,在45天缓冲大小的基础上,应用本文缓冲监控方法、静态缓冲监控方法和相对缓冲监控方法,得出项目绩效指标见表3。未对比动态缓冲监控方法,因为它已被证明在项目后期有更高的延迟概率 [15] 。可以看出,所有方法的实际项目工期都在158天的计划工期内,其中,本文方法的实际项目工期更短,按时完工率更高。这是因为本文方法对缓冲进行了分配,可以将项目经理有限的精力集中在对工期影响最大的活动上,从而达到了更好的绩效指标。活动赶工率上(活动/返工),本文方法活动的赶工率最低,返工的赶工率处于静态和相对缓冲监控方法之间。这是因为活动缓冲区基于PEC进行了分配,并设置了更合理的相对监控阈值,因此只需赶工确需的活动;返工上,由于本文将其视为“不被期望发生的”,并设置了稍激进的静态监控阈值,因此赶工率稍高。总体而言,本文缓冲监控方法在保持相对稳健的项目过程的基础上,获得了更高的按时完工率。

Table 3. Comparison of buffer monitoring methods
表3. 缓冲监控方法比较
综上,本文提出的缓冲管理框架可以获得更合理的计划工期和更优越的绩效指标,显示了本文方法的先进性。
5. 结语
考虑到现代项目返工频发及返工管理工具的缺乏,本文提出了一个返工情境下的缓冲管理框架,试图填补这个空白。首先,提出了利用遗传算法优化活动顺序的想法,以减少项目返工风险;然后,讨论了活动返工的三种基本类型,并提出了各类返工的时间计算公式,从而修正现有缓冲设置方法;接着,充分考虑各活动由于返工而拥有的特征,对缓冲进行了分配和监控阈值设置,从而精细化监控项目实施过程;最后,在一个实际案例上应用了本文提出的缓冲管理框架,结果显示了本文方法的有效性。
本文方法能为返工情境下的项目进度管理提供工具。考虑到现代项目对于“柔性”的需求,进一步的研究可以考虑在现有缓冲管理框架中融入自适应思想,以应对越来越高的环境不确定性。
基金项目
国家自然科学基金(72171177)。
NOTES
*通讯作者。